
The following articles are contained below:-
A
Brief History of Quantum Theory 1925 – Y2K
Fermions and Bosons;
The Janus of Quantum Theory
In
Search of Perfect Symmetry
Quantum
Loop Gravity
"GOD DOES NOT PLAY DICE WITH THE UNIVERSE"
A. Einstein
"EINSTEIN, DON'T TELL GOD WHAT TO DO"
N. Bohr
A Brief
History of Quantum Theory 1925 – Y2K
Part I Inward Bound --- Sub atomic theory
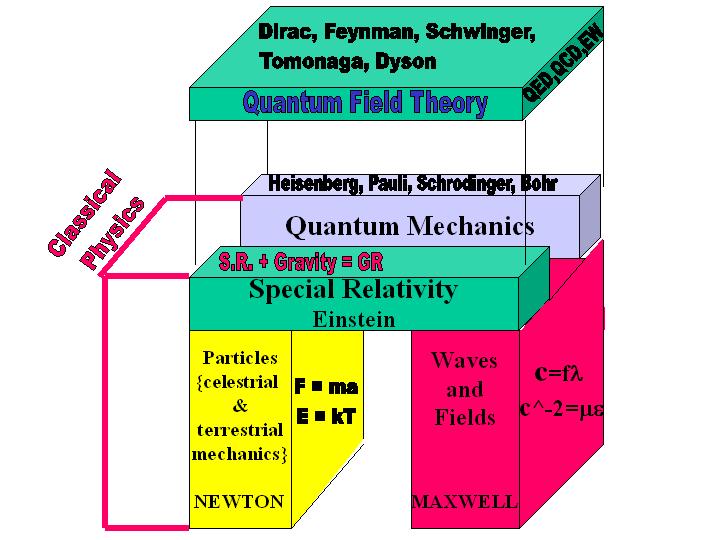
There are 4 formulations of modern quantum theory (QT). Historically
it was Heisenberg’s matrix mechanics, which was first to be published.
The non-commutative nature of matrix multiplication is responsible for
the appearance of his uncertainty principle. Schrodinger’s wave equation
was quick to follow, having delayed publication due to his inability to
produce a fully relativistic version. The nature of the wavepacket that
describes a quantum entity, inherently produces the uncertainty in its
position/momentum (the latter being related to the constituent wavelengths
of the packet via de Broglie’s equation). Dirac showed the equivalence
of both these methods and introduced his own formulation in terms of vectors
in Hilbert space, using his <bra ket> notation. [Hilbert Space was
originally utilized by von Neumann in his attempt to produce a universal
axiomatic formulation for quantum theory]. Dirac was also the first to
formulate a relativistic quantum theory, a union which demanded a field
theory and necessitated the introduction of intrinsic spin and anti-matter!
Finally there is Feynman’s path integral (sum over histories) technique
which is used in the more advanced treatment of interactions of ‘particles’
with their ‘fields’ (whose quanta are fermions and bosons respectively).
If we consider a projectile such as a football, in its motion from the
ground to its position of maximum height, its path is not that of the
shortest route (i.e. a straight line) but rather (half) a parabolic curve.
What is minimised however is its action i.e. it’s (kinetic –
potential) energy integrated over time, (this is known as the principle
of least action). The fact that this so-called Lagrangian formulation
is symmetric (unaltered) over local translations of space and time, yields
the conservation of momentum and energy respectively. According to classical
physics, objects move in a force field, so as to minimize this action
and in just one page of his book, Dirac showed that the sum of the contributions
of the various paths that a quanta can take (each with its own probability
amplitude), reduces to that of the classical stationary action, in the
limit that Planck’s constant ‘h’ tends to zero. In fact
it is due to the small numerical value of h (~ 10^-34 Js) that quantum
effects are not readily observed except at the atomic scale. In other
words the principle of least action is due to quantum mechanics and the
smallness of ‘h’. Feynman later elaborated this in his sum over
histories technique, in which we associate a probability amplitude that
is determined by the action of a particular path, and sum up all of these
to find the overall probability of a quantum moving between two states
(positions). This is schematically shown in the Feynman diagrams but it
is important to realise, that the actual calculations involve the sum
over all the possible paths and not just the particular lines shown in
any given representative diagram.
To first order effects, this technique just retrieves Schrodinger’s
equation. However the power of this method is that we can utilize higher
order perturbations to include the effect of movement (e.g. of an electron),
in a field (electromagnetism), in a way which can also treat the field
in a quantum mechanical manner (involving a photon), thus producing quantum
electrodynamics (QED). [The concept of a force is therefore subsumed by
that of an interaction and in the case of the weak interaction, there
is no force manifested.] The path integral is also important because it
makes quantum theories automatically consistent with special relativity,
providing that the Lagrangian itself is already Lorentz covariant (i.e.
it is not dependent on any one co-ordinate system of 4 dimensional space-time).
Unfortunately these techniques are arduous, as indicated by the fact that
it took 2 teams of mathematicians 4 years to work out one value (it took
one year to discover an error in the calculation)! It did however result
in 3 Nobel prizes but as Weinberg once protested "how can we make
any money out of this".
These perturbation techniques work by first using known exact solutions
(which puts us in the right ball park), and then proceed by making more
fine-tuned approximations. However at each progressively higher level
of energy scale (corresponding to a greater level of complexity of Feynman
diagrams), we need to renormalise our answers to ensure that all
our probabilities again add up to unity. It is a bit like a fractal, in
which approximate measurements of the perimeter of such a shape yields
a different answer, depending on the magnification (energy scale) at which
we carry out the measurement. Hence if left 'unregulated' these perturbation
techniques are inherently divergent, producing infinities in the self
energy of an electron. Renormalization is therefore a necessary technique
of self consistent subtraction, which allows the theoretical values for
the mass, charge and magnetic moment of an electron, to be in agreement
with the experimental values (in particular those of the Lamb shift, the
Lande factor g and the hyperfine anomaly). Much of the work up until 1950
was focused on QED, i.e. the production of a consistent quantum theory
of the interaction of charged particles (electrons) with an electromagnetic
field. Initial steps were undertaken by Dirac with his method of second
quanization (an application of his beloved transformation theory), in
which an electromagnetic field is represented as an assembly of of quanta
(photons). This introduced creation and annihilation operators that obeyed
certain commutational relations which ensured that the particles being
described satisfied Bose-Einstein statistics. This field was not however
relativistic (as is Maxwell's field description) but the method was extended
to classical matter wave fields by Jordan, who introducing the
correct anti-commutational rules, so that the particles (electrons), obeyed
Fermi-Dirac statistics (but this again was not Lorentz covariant). [Jordan
was the first to suggest that the commutational rules that effected the
transition from the classical to the quantum description of a system of
particles, also be applied to a system with an infinite number
of degrees of freedom, that is to a field system.] Henceforth a
quantum field could be interpreted as expressing the probability
of finding a given distribution of particles states throughout space and
time or alternatively an assembly of quanta could be described as a such
a field, thus both the wave and particle nature are incorporated in the
notion of a quantum field! Indeed the other great achievement of Dirac,
was in producing the correct formulation for making quantum theory (QT)
consistent with special relativity (SR) which also demonstrated the necessity
of a field theory. The famous equation that bears his name, not only predicted
the existence of antimatter and it also introduced the mathematical structure
of spinor theory.
Following on from all this endeavor, Heisenburg and Pauli developed a
general method for quantizing (Maxwell's) fields, using the Lagrangian
description and canonical variables (field potential and its conjugate
momenta) but they encountered infinities when they tried to produce a
complete picture of quantum electrodynamics (i.e. QED). The next major
step was the independent work of Tomonaga and Schwinger who described
the interaction of an electron matter field with the electromagnetic field
but due to the effects such as vacuum polarization and the self energy
of the electron, it became necessary to absorb these infinities at each
level of the calculation. Schwinger achieved this by employing Dirac's
contact transformation to eliminate such virtual effects in the calculation.
A different approach was instigated by Feynman, who followed Dirac's philosophy
in regarding electromagnetism as a quantized field but treated
the electron as a quantum particle. In his path integral approach
(which was also inspired by Dirac's work on the usefulness of the Lagrangian
in QT), Feynman applied a relativistic cutoff field (which was equivalent
to an auxiliary field) to cancel the infinite contributions due to the
real particle of the original field. [The auxiliary masses of the cutoff
are used more as a mathematical parameter, which finally tends to infinity
and are nonobservable in principle]. Dirac however had strong reservations
about any theory which neglects infinities instead of infinitesimals (as
does calculus). However renormalization later became a guiding principle
in the formation of the electroweak theory. Finally Dyson demonstrated
the equivalence of Feynman's and Schwinger's method and did much to show
that renormalization was consistent to all levels. [Schwingers method
involved field operators and the calculations were very hard to follow
and indeed had not been pursued beyond a second order, whereas Feynmans
method had been more user friendly]. Dyson managed to recast the Schwinger
formulation so that it displays all the advantages of the Feynman theory
but unlike the path integral method, it used an electon-positron field
and incorporated a term in the Hamiltonian, which described the interaction
of this matter field with the Maxwell field.
Although such approximation techniques are tedious it would be desirable
to utilize Feynmans method for the other 3 interactions (i.e. the weak
and strong nuclear forces and gravity). However unlike electromagnetism,
where the strength with which charged particles couple to their field
is small ~ 1/137, such perturbation techniques are more difficult with
the strong interaction (Quantum Chromodynamics) and gravity has defied
all attempts, since the calculations produce infinities that refuse to
be renormalised. [Gluons interact with themselves as well as with their
quarks, while gravitons, having energy and hence mass, also ‘gravitate’.
Also, gravity is described as a curvature in space-time in general relativity
(GR) – hence a graviton implies a quantised space-time!!!] Interestingly
it is Black holes which offer clues as to how to proceed with a theory
of quantum gravity. The event horizon of such exotic entities can combine
ideas from GR, thermodynamics and QT! The area of the event horizon can
be related to temperature and hence entropy and has given rise to the
development of what is known as the 'holographic principle'. This allows
an explanation of what happens when the information (negentropy) stored
in a (3-dimensional) assembly disappears into a black hole. Eventually
due to Hawking radiation, the material but not the information, is restored
to the universe at large, apparently in violation of the second law of
thermodynamics. This dilemma is avoided if we assume that the information
is stored in the 2-dimensional surface of the event horizon in the form
of string segments (c.f. 'strings' below). Each minute segment
of a string measuring 10E-35 centimeters across, functions as a bit. Hence
the surface of a black hole is able to store 3-D information and is therefore
analogous to a hologram.
On another front, it would also be desirable to collect all the particles
into a multiplet that becomes unified under one interaction, so that the
laws of physics make no distinction between an electron, neutrino or a
quark. Returning to the Lagrangian, certain local gauge (internal)
symmetries, acting upon such a multiple particle state, implies the conservation
of quantum properties but require the introduction of so-called gauge**
fields, in order to ensure the invariance of the Lagrangian under such
(local) transformations. [This involves Noether's theorem, in which symmetries
are related to conservation laws; in particular local gauge symmetries
demand the addition of a gauge field, in order that certain quantum values
are conserved. It is this gauge field that is responsible for the observed
fundamental interaction between the 'particles']. The interactions can
therefore be viewed on a quantum level as gauge (Yang-Mills) fields, that
must be introduced in order to ensure that the Lagrangian of (unified)
particle states are symmetric under localized‘internal’ transformation.
[The quanta of these gauge fields, being the photon, gluon and W, Z particles
of the electromagnetic, strong and weak interactions respectively which
are adequately explained by the 'standard model'. [Technicolour is a provisional
theory which introduces a new interaction analogous to the colour force
that binds quarks and attempts to go beyond the standard model but requires
new generations of particles.] These are mathematically described by specific
groups of transformations. Whereas electromagnetism and the weak
nuclear interaction are successfully unified under a gauge group known
as U(1)*SU(2), the strong nuclear force (Quantum Chromodynamics- QCD)
is described by an SU(3) symmetry. We therefore need to find a master
symmetry group, which subsumes these smaller symmetry gauge groups that
are associated with some of these interactions. Regarding such superunification,
it is not possible to satisfactorily incorporate gravity (which is governed
by the non-compact Poincare group) in what is known as a Unitary representation
(that dictates the other 3 quantum interactions), unless one resorts to
supernumbers, which combines both fermions and bosons via supersymmetry.
[Specifically there is a no-go theorem which states that a group that
nontrivially combines both the Lorentz group and a compact Lie
group cannot have a finite dimensional, unitary representation]. This
concept was originally invoked in the early study of string theory but
although this has received a recent surge in popularity, supersymmetry
itself does not require a string formulation. [Such a Lagrangian, is that
associated with the surface being swept out by a string,
rather than that of a point like particle which, as it moves through
time sweeps out a curve.]
Indeed even without quantum theory, gravity can be regarded in terms
of a local symmetry applied to special relativity
and this puts gravity on an equal footing with acceleration, (where velocity
and therefore the space-time frame of an observer, varies locally with
its 4 dimensional ‘position’). We can therefore apply classical
laws of physics to an accelerating frame of reference, if we invoke a
gravitational field or alternatively a gravitational field can be eliminated
locally by applying an accelerated frame of reference and hence the correct
metric (curvature) of space-time that goes with it. A gravitational field
therefore needs to be invoked, in order to allow the global space-time
transformations of special relativity to be locally symmetric,
thereby extending special relativity to that of general relativity. [In
this respect gravity is said to be locally equivalent to acceleration.]
Likewise the unified electroweak field needs to be invoked, if we are
to allow a local gauge transformation to act symmetrically on a family
of leptons or quarks. However whereas Feynman’s path integral technique
is applicable to these interacting particles, when considering gravity,
it is not possible to use such accurate quantum techniques, since the
calculations blow up into infinity and refuse to be renormalised. It is
therefore hoped that by extending unification to include all 4 interactions
some of these infinities will cancel out without the need for messy renormalisation
tricks.
So from the simple description of nature in terms of classical particles
and fields, we have been forced to accept their description in terms of
quantum theory. Group symmetry allows us a way of relating a collection
of these particles, with the corresponding fields with which they interact
with one another. Whereas Newton's gravitational law united falling bodies
on Earth with celestial motion, Einstein unified space, time and gravity,
while Maxwell succeeded in unifying Magnetism with Electricity. Gauge
symmetry provides a way of combining both electromagnetism
and the weak interaction and allows
a way of extending this description so as to include the strong
interaction (the so called standard model). However this effort has not
achieved the status of a complete unification, since we have not yet discovered
a single group, that encompasses all three
interactions.(i.e. a Grand Unified Theory). Supersymmetry hopes to put
the quanta of both ‘particle’ and ‘field’(i.e. fermions
and bosons), on an equal footing, while the latest development -- string
theory, hopes to explain what symmetries are allowed, which in turn determine
the conservation laws of physics. [Whereas bosonic fields behave in a
conventional commuting manner, the fermionic field is a spinor representation
of the Lorentz group and are consequently anticommuting!]. As an extra
bonus, putting fermions and bosons in the same super multiparticle state,
necessitates the introduction of a gravitational field (i.e. local supersymmetric
transformations invoke a field that produces the localised space-time
translations that is indicative of gravity). The price that we have to
pay for such a ‘simplification’ of physical phenomena into a
unified framework, is ironically, a succession of layers of abstract concepts,
together with their relevant mathematical structures. Hence from tangible
atoms, we move by one level of abstraction to invisible fields and particles.
A second level of abstraction takes us from fields and particles to the
(gauge) symmetry-groups by which fields and particles are related. The
third level of abstraction, is the interpretation of (super) symmetry-groups
in terms of states in higher (10) dimensional space time, since it is
the manner in which the space is compactified which determines the symmetries
that are permitted. The fourth level is the world of superstrings by whose
dynamic behavior the states are defined. Finally we arrive at M-theory,
in which even the strings are regarded as just one of many possible p-branes
that can exist in a 11-Dimensional space-time. M-Theory consequently contains
many varied multiverses, of which our own particular universe permits
such rich laws of physics, that it allows our very existence so that we
can perceive it!
* * * * * * * * * * * * * * * * * * * * * *
Part II Outward Bound ----- Cosmology
Quantum theory, has been used to apply a wavefunction to the universe
as a whole (viz. The Wheeler De Witt equation), even though we are lacking
a quantum theory of gravity. Such quantum cosmology has been used by Hawking
et al, in order to help explain the ripples in the big bang radiation
detected by COBE and to possibly explain how quantum wavefunctions can
undergo decoherence to produce a classically observable universe.
In the absence of a quantum theory of gravity, provisional
Grand Unified Theories (GUTs) have provided an understanding as to
why the universe is so smooth (homogeneous) and is so close to the critical
density that would eventually halt its expansion, (referred to as the
horizon and flatness problem respectively). In GUTs, the electroweak theory
and the strong force QCD, are unified into one interaction and the underlying
laws of physics make no distinction between an electron, neutrino or a
quark. [In math speak, the SU(3)*SU(2)*U(1) gauge symmetry of the 'standard
model' are unified under one larger symmetry group]. This symmetry between
these particles (and their interactions) only becomes broken into the
separate interactions that we observe around us today by a mechanism,
which involves the so-called Grand Unified Higgs fields (different from
the electroweak higgs field).. The spontaneous symmetry breaking (SSB)
of the Higgs mechanism gives the particles their distinctive properties
and their interactions different coupling strengths and ranges. In other
words the distinction between strong, weak and electromagnetic interactions
is caused by the way that their force carrying particles (i.e. gluons,W,Z
and photons) interact with the different Higgs particles.
The simplest GUT requires 24 Higgs fields but 2 Higgs fields can be represented
as a 3 dimensional graph, which resembles a sombrero hat! It has the unusual
property that its zero value has a (local) maximum energy density (centre
of hat), while it achieves zero energy density at the rim, where the Higgs
field is not at the origin (i.e. it is non zero), and it is here which
corresponds to the SSB condition. When this SSB occurred in the very early
universe, the Higgs fields aligns itself in a particular direction (analogous
to a ball rolling down the sombrero to the brim in a spontaneously chosen
direction) and the direction would be randomly chosen in different parts
of the universe, which are sufficiently far apart. Such a mismatch in
directions would correspond to a large number of magnetic monopoles being
formed, which unlike electric monopoles (e.g. electrons) are not observed
in our universe.[North and south poles occur together and are not observed
separately, although Maxwell’s equations of electromagnetism would
be more symmetric if we included such sources.]
This is where Inflation(cf. addendum below) comes into
play, since it allows us to alter the graph in a way that produces a dip
(or a flattened top) in the centre of the ‘sombrero’ which corresponds
to a false vacuum. This false vacuum allows the alignment of the Higgs
fields that are responsible for SSB, to grow gradually rather than produce
a more chaotic distribution, which would result in the production of too
many magnetic monopoles. As the name suggests, the false vacuum has peculiar
properties, but the important point is that although it has a very high
positive energy density, it has a far (~ 3 times) higher negative pressure
and therefore corresponds to a repulsive force according to Einstein’s
general theory of relativity. [Note that it is not the uniform negative
pressure that drives the expansion, since only pressure differences result
in forces, but rather that pressure like mass, gives rise to gravitational
forces and negative pressure gives rise to a negative repulsive gravity
that is associated with a cosmological constant]. Hence when we have a
SSB of a Higgs field coupled to gravity we generates a constant term,
which corresponds an increase in the energy density of the vacuum which
cannot be ignored when dealing with GR! Einstein originally introduced
such a cosmological constant (lambda)** into
his early model of the universe, which was then believed to be static,
and hence the positive gravitational attraction of all the matter of the
universe had to be balanced by a repulsive term. The introduction of such
a term into the era when GUTs prevail, does however produce an exponentially
inflating universe (the de Sitter solution), rather than the one we
observe today that is typical of an initial explosion of matter, which
is experiencing the decelerating effects of gravity. Incidentally the
cosmological constant in the universe today is known to be close to zero,
although quantum calculations involving GUTs produce an embarrassingly
large value for lambda.
Recent observations of supernova in distant galaxy clusters indicate
that it has a small positive value, which consequently produces a repulsive
5th force, whose effects only become significant over large
volumes of space. If these observations are indeed valid, it shows that
the universe is undergoing acceleration and will never halt its expansion.
The good news is that this explains the flatness of the universe without
needing to invoke such a large value of the 'missing mass'. The larger
the cosmological constant, the smaller he amount of positive mass/energy
that is needed to produce a flat but not closed universe (Omega =1). Some
modern notions have tried to do away with the somewhat ad hoc
inflationary theory by allowing the value of lambda to decrease
with time. The early universe thus underwent rapid expansion due to the
large initial lambda value, which itself is not stable but decreases with
time. This theory allows for a fine tuning, and as the universe expands
and lambda decreases, matter is created in just the right amounts to keep
the density of the universe sufficient for it to maintain its flat value.
The problem with this theory is that it requires the universal speed of
light to be coupled to lambda and decrease with time!! Such an iconoclastic
notion as the speed of light being reduced as the universe expands, will
require a good deal of empirical evidence that is not easy to produce.(C.f.**
below). An alternative approach is to introduce another quantum field
called Quintessence, which is a basic (more adaptive) property of 'empty'
space that may be able to account for the 5th force of repulsion.
So historically inflation was used to explain the dearth of magnetic
monopoles. However by incorporating such a brief but rapid expansion
in the early universe, we can also allow for our observable universe
to have been causally connected in the past and these effects can
explain the flatness and the horizon problem respectively. The false vacuums
allows the Higgs fields to grow in alignment without too much chaos, therefore
avoiding the creation of too many magnetic monopoles, before they quickly
decay into the true vacuum (via quantum funneling) that we observe today.
Unfortunately, calculations involving the growth and percolation of these
false vacuums have encountered difficulties and several refined variations
of inflation theory have had to be introduced. In addition, if we resort
to string theory, it needs to be embedded in 26 dimensions that became
compactified during the early SSB period, when the false vacuum collapsed
(as if things aren’t complicated enough).
It therefore becomes necessary to study the actual space in which the
field equations exist. Whereas the mathematics of group theory was required
by the physicists of the 60’s, topology has also become necessary
for those studying how higher dimensional universes become curled up to
produce our observed 4 dimensions of space-time. What’s known as
the cohomolgy properties of these compactified spaces, are related to
the number of generations (viz 3) of quarks and leptons that can
occur, as well as the symmetries that are permitted (this number
equals half the Euler characteristic of the manifold). This prompts a
small digression, in that Penrose employs a sheaf version of cohomology
in his twistor** theory. His philosophy
is that both quantum theory and general relativity need to be replaced
by a single and more fundamental theory, one which would replace the space-time
description of physics, with that of a space of complex numbers associated
with spinor mathematics – projective twistor space. Spacetime
and twister space are related by a correspondence that represents light
rays in spacetime as points in twister space. A point in spacetime is
then represented by the set of light rays that pass through it (each having
a 'null direction'). Thus a point in spacetime becomes a Reimann sphere
(a well known method of steriographically representing a complex plane)
in twister space and the effect of Lorentz transformations produce congruences
that twist (hence the name). In this way we consider spacetime to be a
secondary concept and regard twister space (initially the space of light
rays) to be a more fundamental space.
The actual twister coordinate, is constructed out of a pair of two-spinors
which obey certain relationships to each other, that are dictated by the
corresponding spacetime coordinate (the spinors satisfy a specific twistor
differential equation). Now if we think of light rays as photon histories,
we also need to take into account their energy and also its helicity which
can be either right or left handed or zero. The multiplication of a twister
by its conjugate yields twice the value of its helicy or twist, which
can therefore be either positive , negative or zero. [This then leads
to the formation of a projected twistor space, in which the full
twistor space is projected into a space which is divided into the three
regions according to whether their helicy is positive, negative or zero].Twister
theory is a conformal (i.e. scale invariant ) theory, in which physical
laws that are usually written in the framework of space-time, are expressed
in what may turn out to be a more fundamental and revealing manifold,
which could therefore yield a more fundamental understanding of physics.
A massless field is then defined by a contour integral in twistor space
and these integrals are determined once we know about the singularities
of a general twistor function in twistor space (in the case of electric
or magnetic fields these singularities look like charges or sources where
field lines begin or end). In other words, the differential equations
that describe fields in space time have been reduced to simple functions
in the geometry of complex spaces, viz. projective twistor space. The
field is given by the contour integral around this function which in turn
is determined by the nature of the singularity of this function, (hence
the use of sheaf cohomology in dealing with the analysis of these regions).
For massless fields, it turns out that the helicity of the quantum particle
H is related to the homogeneity of the twister field T by the simple relationship;
H=h/2 (-2-(T)), so if we have a photon of spin +1 it is necessary to write
down a twister function of general power of 4 while for a -1 helicity
photon the homogeneity must be 0. (for a H=+2 graviton, T=6). We therefore
have a fundamental distinction between left and right handed light i.e.
chiral asymmetry is a fundamental property of twister theory!
Producing a quantum theory of gravity is particularly difficult for
several reasons. Firstly quantum gravity implies quantised space time!!!
Secondly gravity is intrinsically so weak it has not yet been possible
to detect classical gravitational waves, let alone its graviton (it is
also difficult to combine the two realms, since QT deals with very small
scale phenomena, while GR deals with large masses). Thirdly, quantum field
theories are written as spinor fields, to which, the Riemannian techniques
of GR not applicable Finally regarding unification, the GR group structure
is non compact, while QT group is Unitary and there is a theorem which
states that there is no finite unitary representation of a non compact
group (this is why we have to resort to supernumbers). At first glance
GR and QT look very differently mathematically, as one deals with space-time
and direct observables while the other with Hilbert space and operators.
One approach to synthesizing the two and providing a quantum theory of
gravity, involves Topological Quantum Field Theories (TQFT). [A topologist
is sometimes defined as a mathematician who cannot tell the difference
between a tea cup and a doughnut, since they are diffeomorphic to each
other, both having a genus of 1 ]. Quantum states are given topologies
and cobordism allows a description of how quantum (gravity) states evolve
i.e. TQFT maps structures in differential topology to corresponding structures
in quantum theory. The state of the universe can only change when the
topology of space itself changes and TQFT does not therefore presume
a given fixed topology for space-time. Quantum operators are therefore
related to cobordism and n-category theory (i.e. algebra of n-dimensions)
is a useful advance in understanding the cobordism theory of TQFT.
There have been two reactions to the apparent inconsistency of quantum
theories with the necessary background-independence of general relativity.
The first is that the geometric interpretation of GR is not fundamental,
but just an emergent quality of some background-dependent theory. The
opposing view is that background-independence is fundamental, and quantum
mechanics needs to be generalized to settings where there is no a-priori
specified space-time. This geometric point of view is the one expounded
in TQFT. In recent years, progress has been rapid on both fronts, leading
ultimately to String Theory (which is not background independent)
and Loop Quantum Gravity (LQG), which is background independent
and also incorporates the diffeomorphic invariance of GR. Topological
quantum field theory provided an example of background-independent quantum
theory, but with no local degrees of freedom, and only finitely
many degrees of freedom globally. This is inadequate to describe gravity,
since even in the vacuum, the metric has local degrees of freedom according
to general relativity (e.g. those due to the propagation of gravity waves
in empty space).
Loop Quantum Gravity is a nonperturbative quantization of 3-space geometry,
with quantized area and volume operators. In LQG, the fabric of space-time
is a foamy network of interacting loops mathematically described by spin
networks (an evolving spin network is termed a spin foam; spin foams are
to operators what spin networks are to states/bases). These loops are
about 10E-35 meters in size, called the Planck scale. In previous lattice
theories the field is represented by quantised tubes/strings of flux which
only exist on the edges of the lattice and the field strength is given
by the value of integrating around a closed loop. In LQG space
and time are relational! As in GR where there are many ways of slicing
a section of space time, there are many ways of slicing an evolving spin
network - thus there are no things only processes! [A spin network is
a graph with edges labeled by representations of some group and vertices
labeled by intertwining operators. Thanks in part to the introduction
of spin network techniques, we now have a mathematically rigorous and
intuitively compelling picture of the kinematical aspects of loop quantum
gravity.] The loops knot together forming edges, surfaces, and vertices,
much as do soap bubbles joined together. In other words, space-time itself
is quantized. Any attempt to divide a loop would, if successful, cause
it to divide into two loops each with the original size. In LQG, spin
networks represent the quantum states of the geometry of relative space-time.
Looked at another way, Einstein's theory of general relativity is a classical
approximation of a quantized geometry.
Historically, Regge calculus was the first attempt to quantize gravity,
by dividing up space into small (flat) 3D tetrahedral simplexes, in which
the curvature is concentrated along their boundaries. From this Hilbert
space of quantum tetrahedron, it was intended to produce 'Feynman propagators'
for gravity and recover Einstein's field equation in the macroscopic domain
of space-time. Each of the edges is associated a spin j and in one type
of approach, the exponential of the action in such a configuration, is
a suitable product of the the 6j symbols associated to each of the 6 edges
of the 3-simplexes and a partition function is obtained by taking the
sum of this products over the possible associations of the spin to the
edges. Remember that angular momentum is a quantum (bi)vector and is therefore
subject to Heisenberg' Uncertainty Principle. [In considering a Lorentzian
(as opposed to a 3-D) spin network we employ a 4-simplex in which there
are 4 tetrahedra, 5 vertices, 10 triangles and 10J symbols].
Next consider Wilson loops, which have been used to analyze fields in
QCD by means of applying a lattice structure and integrating along closed
paths. They are functions on the space of connections; at a lattice
point the Wilson loop is just the trace of holonomy around the loop on
the lattice, taken in some representation of the holonomic group of the
gauge field. [This philosophy originated from considering the vacuum as
being like the discrete lines of (magnetic) flux that is exhibited by
superconductors.] A 'connection' on the lattice is simply an assignment
of an element of a gauge group to each edge of the graph, representing
the effect of a parallel transport along the edge. [The holonomy around
such a gauge field, is a measure of the field strength, which in turn
determines the value of the Feynman path integral]. Each edge of this
lattice is assigned a gauge group element that represents the (holonomic)
connection and the vertex is also assigned a group element that represents
a gauge transformation. From this a quotient space is formed (i.e. the
space of connections modulo gauge transformations), and by mapping these
onto suitable(complex) irreducible spin representations, we obtain a suitable
way of producing a Spin Network. [Such spin network edges represent
quantized flux lines of the field]. Holonomy is a natural variable in
a Yang-Mills gauge theory, in which the relevant variables do not refer
to what happened at a point but rather refers to the relation between
different points connected by a line (curve). Hence to create a framework
for quantum GR we introduce a connection A and a momentum conjugate E,
from which we can produce a spin network together with area and volume
operators, which act upon space so as to quantise it. [The flux through
a surface is represented by area operators for a spin network, acting
on a surface described by a spin network basis]. In LQG, holonomy
becomes a quantum operator that creates loop states. Over a continuous
background, Wilson loop states are far too big to produce a basis of Hilbert
space of a QFT. However loop states are not to singular or to many when
formulated in a background inependent theory, where spacetime is itself
formed by loop states, since the position of these states is relative
only with respect to other loops and not to the backlground. Therefore
the size of the space is dramatically reduced by this diffeomorphic invariance
(a feature of GR itself).
A finite linear combination of loop states are defined precisely as spin
network states of a Yang-Mills theory. Spin networks are gauge invariant
and by taking suitable sums of tensor products, provide an orthonormal
basis for LQG. Penrose had earlier introduced Spin Networks, in which
the edges were labeled by an irreducible representation of a SU(2) Lie
gauge group (characterized only by its dimension d =2j+1, where j is the
quantum spin number) and the vertices with intertwining operators
(tensors that transform incoming states into the outgoing states) and
it was found that such a combinatorial formalism was preferable since
it produced a relational theory. Spin networks have edges which are associated
with a spin j quantum of action and the number of edges intersecting at
a node determines its area, while the volume is determined by the number
of nodes in a given region. A strict connection exists between quantum
tetrahedra and 4-valent vertices of SU(2) spin networks. The 4 faces
of a tetrahedron are associated with 4 irreducible representations of
SU(2), which are represented by a perpendicular line, the 4 of which meet
at a central node of the tetrahedron (there are actually bivectors associated
with each face, in keeping with constraints of GR relating to the Ricci
curvature tensor --- quantizing the bivectors/tetrahedra amounts to labeling
each face with a pair of spinors). We therefore obtain a 4-valent (colour
coded) spin network (each line of which represents a quantized unit of
action, while the nodes behave as area operators), which can exhibit properties
that are gauge invariant. The quantum bivectors allow us to construct
area and volume operators which act upon the spin network basis to
produce a discrete spectrum which has units of Planck length squared and
cubed respectively (in the case of the area operator, the eigenvalues
are 1/2sqrt (j(j+1)) and as in keeping with quantum theory we would expect
these to correspond to physical observable i.e. we have a quantized space!
These spin networks (formed from the above mentioned quotient gauge space),
do not refer to a specific space background and we can reproduce Wilson
loop calculation to imitate a quantum theory of gravity, which is relational,
as in the spirit of GR. So, since spin networks form a convenient basis
of kinematical states, they have largely replaced collections of loops
as our basic model for 'quantum 3-geometries'. Now in order to better
understand the dynamical aspects of quantum gravity, we would also like
a model for 'quantum 4-geometries'. In other words, we want a truly quantum-mechanical
description of the geometry of spacetime. Recently the notion of 'spin
foam' has emerged as an interesting candidate; so whereas spin networks
provide a language for describing the quantum geometry of space, a spin
foam attempts to extend this language to describe the quantum geometry
of space-time. A spin foam is a 2-dimensional cell complex with faces
labeled by representations and edges labeled by intertwining operators;
generically, any slice of a spin foam gives a spin network. We calculate
the amplitude for any spin foam, as a product of the face and edge amplitudes
(which equate to propagators) and the vertex amplitudes (which equate
to intersection amplitudes). [Abstractly, a Feynman diagram can be thought
of as a graph with edges 'labelled' by a group representation and vertices
labelled by intertwining operators. Feynman diagrams are 1D because they
describe particle histories, while spin foams are 2D because in LQG, the
gravitational field is described not in terms of point particles but as
1D spin networks. Feynman computes probability in terms of probability
amplitudes for edges and vertices whereas spin foams compute probability
amplitudes as a product of faces, edges, and vertices amplitudes. Like
Feynman diagrams spin foams serve as a basis for quantum histories.]
Although QLG has been successful in predicting Hawking radiation and
Black Hole entropy, it is restricted to the domain of quantum gravity
and as yet does not offer any import on the other fundamental interactions
or the possibility of unification. Unlike string theory it does however
offer testable predictions, such as the variation of the speed of light
at different energies. The spin foam which makes up the fabric of space-time
predicts a varying refraction coefficient depending on the frequency and
hence energy of the photon. It is therefore hoped that by studying gamma
ray bursts from the most remote regions of the universe, this small dispersion
in the arrival times of the radiation can be observed (other avenues of
research also point to theories involving a variable speed of light).
Some researchers believe that even the success of string theory can be
explained in terms of discrete units of space that become evident on the
Planck scale (which being ~ 10 E -35m, is much smaller than that of the
compactified dimensions of superstring theory). Also both theories allude
to a version of the Holographic**
principle (where a bulk theory with gravity in n dimensions, is equivalent
to a boundary theory in n-1 dimensions without gravity, cf. Maldacina
conjecture below), in which entities such as black hole contain all their
information in their Event Horizons - one bit for every 4 Planck areas.
This arises since black holes emit Hawking radiation and therefore its
mass is related to a thermodynamic temperature, hence the entropy of a
black hole is proportional to its surface area while information is negentropy.
However LQG emphasize the necessity to have a relational theory
in which space and time are dynamic rather than fixed and the primary
concept is that of processes by which information is conveyed from one
part of the world to another. Hence the area of any surface in (QLG) space
is nothing but the capacity of that surface as a channel of information
and so the world can be construed as a network of relationships. This
avenue of approach has lead to the study of a relational logic called
Topos theory and non commutative geometry, in which it is impossible
to determine enough information to locate a point (a point is then described
by an appropriate matrix) but it can support a description of particles
and fields evolving in time)
Hawking on the other hand believes that QT of supergravity is the way
forward, although he does utilize an imaginary time coordinate. Time has
been a problem for philosophers and more recently, physicists have started
to take the view that our concept of time may be responsible for some
of the intractable problems that face QT and GR (particularly relating
to the collapse of the wavefunction but also a QT of gravity implies quantized
space-time). Indeed J. Barbour believes that time does not exist but is
merely a mental construct. He has a tentative theory which involves a
stationary cosmological wave functions (akin to that used in the Wheeler-
De Witt equation) acting upon a configuration space of the whole universe
(known as Platonia). Einstein once said that space and time are modes
by which we think rather than conditions in which we live, but as Hume
would say how can something that exists as a series of states (the Nows)
be aware of itself as a series? Of course in the cosmic wavefunction,
we must also include the human mind but I am still not convinced that
this will be sufficient to completely justify Barbour’s claim of
‘The End of Time’ in physics.
Returning to string theory, five versions originally evolved but more
recently, a ‘second revolution’ has subjugated these into an
11 dimensional formulation known as M-theory which also accommodates supergravity!
(M stands for mystery, as very little is known about the underlying nature
of this 21st Century theory). As T.S. Eliot once wrote, "trust
the tale not the teller", hence even if the models that are proposed
appear incredulous, the mathematics may hold real value.
To summarise therefore, inflation theory is good example of where studies
in sub-atomic physics are relevant to those of cosmology. When we study
the quantum mechanics of GUT and add on the effects of general relativity
as an appendage, we find that it necessary to include a non-zero value
for the cosmological constant for the early universe, when strong, weak
and electromagnetic interactions were unified. This produces an exponentially
inflating universe during this early phase transition, which overcomes
the horizon, and flatness problems. Its main raison d’ętre
was however to explain the scarcity of magnetic monopoles. These would
otherwise be more prevalent if there had been a more chaotic Higgs mechanism,
rather than the inflationary version of the SSB that is responsible for
the distinct interactions that we observe today. The richness of these
physical laws is nowhere more evident, than in the creation of our own
planet Earth and in particular, the evolution of the human mind, which
allows contemplation of the very laws that are responsible for its existence.
Addendum
** In some sense complex numbers
are more fundamental than real numbers. The extra mathematical structure
gives rise to theorems like Cauchy's integral formula, which demonstrates
an interplay between local and global (topological) properties of a manifold
and this has been exploited to great effect in twistor theory. [This could
have relevance to the non-locality involved in the actual collapse of
a wavefunction or the fact that the negative energy stored in an gravitational
field is also non local] There are also local isomorphisms between space-time
groups and those groups associated with complex spaces (the latter, as
in the case of spinor space, is simply connected, while the rotational
group of Euclidean geometry is doubly connected). Indeed quantum
mechanics demands a complex space (that of spinors) in order for it to
be compatible with SR, this being part and parcel of quantum field
theory. Now a spin n/2 field, which is represented by a symmetrical spinor
with n indices, can be associated (in Projective Twistor
space), with a twistor function f{-n-2} of homogeneity {-n-2} via a contour
integral. One of the most natural ways in which complex analysis and contour
integral techniques can be developed, is to consider sheaf theory and
sheaf cohomology, which takes a fundamental role in twistor theory. More
precisely, zero rest mass fields on space-time, which are originally described
as real spinor fields satisfying field equations, can be expressed as
arbitrary holomorphic functions of a twistor (with contour), and these
can then be further interpreted as elements of a (first) sheaf cohomology
group. [Historically, it was the study of sheaf theory, which originally
gave rise to CATEGORY theory, in an attempt to determine which given sheafs
are equivalent. For example, a presheaf of abelian groups over a topological
space X, is a contravariant functor on the category of open subsets of
X]
**The cosmological constant Lambda acts
like a (positive) vacuum energy density but is associated with a negative
pressure because;
1. The vacuum energy density must be constant because there is nothing
for it to depend upon.
2. If a piston capping a cylinder of vacuum, is pulled out producing
more vacuum, the vacuum within the cylinder has more energy, which must
have been supplied by the force pulling on the piston.
3. If the vacuum is trying to pull the piston back into the cylinder,
it must have a negative pressure, since a positive pressure would tend
to push the piston out.
If we denote the ratio of the vacuum density/critical density as Kappa
and the ratio of the actual matter density /critical density as Omega,
then obviously the Universe is open if Omega + Kappa is less than unity,
closed if it is greater than unity and flat if it is exactly one. Now
if Kappa is greater than unity then the Universe will expand forever unless
Omega is much larger than current observations suggest. For Kappa greater
than zero even a closed Universe can expand forever (e.g if the
density of matter is as small as we currently observe).
MORE DETAILS REGARDING INFLATION
The electroweak Higgs field, is responsible
for spontaneous symmetry breaking and gives mass to particles such as
the W and Z particle. In supersymmetry theory it is believed to be responsible
for giving mass to all the particles, depending on how strong it couples
to each of them. The Grand Unified Higgs mechanism may also explain the
nature of the rapid inflation experienced during the earliest epoch of
the universe, since its initially high energy value can be associated
with a negative pressure which drives the expansion. When the energy of
the vacuum drops to zero (being converted into matter and radiation),
the Higgs field takes on a non zero value, which breaks the symmetry of
the known interactions by giving mass to the particles and their force
carrying bosons. This inflation field solves the cosmological problems
of flatness, monopole scarcity and the horizon problem. and was derived
from a consideration of the adding Einstein’s field equation to GUT.
During this inflationary epoch which lasted for only a billionth of a
a billionth of a a billionth of a second a region the size of a DNA molecule
would have expanded to the size of the Milky Way galaxy - - a greater
expansion than that that has occurred during the remaining 13.7 billion
years of the universe. Only by ’vaporizing the vacuum’ by returning
it to a temperature high enough to evaporate the Higgs field (causing
it to have a zero average value throughout space), would the full symmetry/unification
become apparent again.
According to theory, matter and radiation are produced at the end of
inflation and however, whereas these decrease in energy as the universe
expands, the inflationary field actually increases its energy (sapping
energy from the expansion like a rubber sheet that is expanding), since
it initially has a constant density as it expands. As the universe expands,
matter and radiation lose energy to gravity, while an inflation field
gains energy from 'repulsive' gravity. In this way we can account for
the large amount of matter that is present in the universe today, by just
considering a small amount of matter (~20 pounds) that originated in a
tiny space (10^-26cm diameter), as the inflationary phase grew to a close.
This is because at the onset of inflation, the field didn't need to have
much energy, since the enormous expansion it was about to sporn would
enormously amplify the energy it carried. [This is in contrast with the
standard big bang model in which the initial energy content of the universe
would need to be enormous, due to its high energy content] hence inflationary
cosmology, by 'mining' gravity can produce all the ordinary matter and
radiation that we see today from a tiny speck of inflationary filled space.
Note also that small quantum fluctuations in the early inflationary Higgs
field arise due to Heisenbergs uncertainty principle and these can explain
the seeding of the universe with inhomogeneities that coalesced
to form present day galaxies. This theory is in close agreement with recent
analysis of Cosmic Background Radiation.
Inflation also rescues the problem regarding why there is a low entropy
in the early universe, which gives rise to 'the arrow of time'. During
the inflation epoch the residing field made gravity repulsive, which meant
that any clumpiness in the fabric of the cosmos (due to Heisenberg's UP),
was expanded so rapidly and to such an extent, that it these warps became
stretched quite smooth. Also because of this rapid expansion of space
the density of matter also became very diluted. This is in direct contrast
to the post inflationary period where the attractive force of gravity
would tend to cause the creases of space and clumping of matter to increase.
At the end of the inflationary period, the universe would have grown enormously
removing most of the nonconformitiey, and as the field reached the bottom
of the potential energy well, it converted its pent up energy into a nearly
uniform bath of particles. Hence this smooth uniform spatial expansion
of matter that results in the inflation model explains why the universe
started with a relatively low entropy state. In actual fact the overall
entropy increases during inflation (in keeping with the second law of
thermodynamics), but much less than it might have been, since the smoothing
has reduced the gravitational contribution to entropy (uniformity and
reduced clumping means less entropy -- black holes being the most extreme
case of clumping having the greatest entropy). When the inflationary field
relinquished its energy it is estimated to have created 10^80 particles
of matter and radiation and this would correspond to an enormous increase
in entropy. So even though the gravitational entropy went down this was
more than compensated by the creation of more particle states in accordance
with the second law of thermodynamics. The important thing is however
that inflationary expansion/smoothing of the universe created a huge gap
between what the entropy contribution of the universe was and might have
been, thus producing a low entropy in the early universe. This then set
the stage for a billion years of gravitational collapse (increasing entropy),
whose effects produced the seeding of galaxies and the formation of stars
that we continue to witness, as the arrow of time moves forward.
In the above considerations it is necessary to assume that prior to
inflation there was a typical high entropy space which was riddled with
warps and that the inflationary field was highly disordered with its value
jumping around due to quantum uncertainties. [Remember that the UP relates
to the complementary uncertainties in a particles position and momentum
(~ rate of change of positioned) and when applied to fields, it implies
that the more we know about the value of a field (number of particles
at a location),.the less we know about its rate of change at that location].
Hence we can expect that sooner or later a chance fluctuation within this
turbulent highly energetic preinflationary period, will cause the value
of its field to jump to the correct value in some minutel region of space,
and in so doing initiate an outward burst of inflationary expansion. Now
this understanding is actually close to Boltzmann's suggestion, that what
we now see is a result of a rare but every so often expected fluctuation
from total disorder. The advantage here however, is that only a small
fluctuation within a tiny space during the inflationary period, is necessary
to yield a huge and highly ordered universe that we now observe. A jump
to lower entropy within a tiny space was leveraged by inflationary expansion
into the vast reaches of the cosmos. Thus inflation doesn't just explain
the horizon problem and the dearth of magnetic monopoles, it also accounts
for the low entropy of the early universe (arrow of time) the flatness
of space and the slight inhomogeneities from which galaxies formed. Indeed
it is also conjectured that such a sprouting of an inflationary universe
could be common enough to occurred elsewhere during the chaotic primordial
state of high entropy and may continue to do so, repeatedly sprouting
new universes from older ones, creating a multiverse (each maybe with
different subsequent laws of physics which evolved at various symmetry
breaking phases). Note that in order to artificial create conditions for
such a universe, we would have to cram about 20 pounds of inflationary
field into a space of about 10^-78 centimeters cubed which means a density
of 10^67 times that of an atomic nucleus.
In summary, through a chance but every so often expected fluctuation
of a chaotic (high entropy) primordial state, a tiny region of space achieved
conditions that lead to a brief burst of inflationary expansion. The enormous
rapid expansion resulted in space being stretched tremendously large and
extremely smooth. As this burst drew to an end, the inflationary field
relinquished its huge amplified energy by filling space nearly uniformly
with matter and radiation. As the inflation's repulsive gravity diminished,
ordinary attractive gravity became dominant. Gravity exploits tiny inhomogeneities
caused by quantum fluctuations that are inherent in Heisenberg's UP, and
causes matter to clump, forming galaxies and stars and ultimately leading
to the formation of solar systems such as our own. After about 7 billion
years repulsive gravity once again became dominant but this is only relevant
on largest of cosmic scales and the nature of this dark energy and indeed
the known dark mater is as yet unknown.
Footnote: . . There are still many fine tuning problems with inflation,
and as such inflationary cosmology is not a unique theory and many different
versions have been proposed. These include ; Old inflation, new inflation,
warm inflation, hybrid inflation, hyper inflation, assisted inflation,
eternal inflation, extended inflation, chaotic inflation, double inflation,
weak inflation, hypernatural inflation
**The historic sequence for this is as
follows;
Hawkings originally showed that the area of a black hole can never decrease
in time, suggesting that it is analogous to entropy. Bekenstein argued
that this relationship was more than just an an analogy and that a black
hole has an actual entropy that is proportional to its area. However entropy
is related to temperature (~S = ~Q/T)and this was not a property that
was associated to black holes at that time. Hawkings then went on to discover
that a black hole emits radiation and can be given a temperature that
is inversely proportional to its mass (and the mass of a black hole directly
determines its event horizon). Hence the entropy of a black hole can be
shown to be S =1A/4hG and when object fall into a black hole the entropy
of the surrounding universe decreases (since negentropy is a measure of
information which is reduced when objects disappear,) while that of the
black hole increases so as to maintain/increase the overall value. On
the other hand if the black hole radiates energy, it loses surface area
and hence entropy but the entropy of the outside world will increase to
make up for it. However the entropy that is removed when a highly organized
system is dropped into a black hole, is much less that the increase of
entropy that is returned, when the black hole radiates that amount of
mass back to the universe, thus implying an overall increase in entropy,
in keeping with the second law of thermodynamics. Bekenstein later went
on to assert that the amount of information that can be contained in a
region is not only finite but is proportional to the area bounded
by that region, measured in Planck units (Holographic principle) and this
implies that the universe must be discrete on the Planck scale. This Bekenstein
Bound is partly a consequence of GR and the 2nd law of Thermodynamics,
but the argument can be turned around, and it can be shown that assuming
the 2nd law and the Bekenstein Bound, it is possible to derive GR. Hence
we have 3 approaches to combining GR with QT viz String theory, LQG, and
black hole thermodynamics and each of these indicate (in differing ways)
that space and time are discrete (the last two are also relational based).
More recently, new difficulties have become evident, from the fact that
when (organized) objects drop into a black hole, their quantum wave functions
are in a pure (correlated) state, while when the Black Hole eventually
evaporates, the radiation is in a mixed quantum state (i.e. the individual
quanta are not correlated as in an assembly of bosons or fermions). Now
a pure state cannot evolve into a mixed state by means of
a unitary transformation, which is a problem since unitary transformations
are a crucial feature of all quantum wavefunctions (in order that probabilities
evolve in a correct manner). Hence we need to find a way of reconciling
this dilemma, perhaps by invoking a non unitary theory or by discovering
a way of accounting for the extra information that a pure state has in
comparison to a mixed state. If the correlations between the inside and
outside of the black hole are not restored during the evaporation process,
then by the time that the black hole has evaporated completely, an initial
pure state will have evolved to a mixed state, i.e., "information"
will have been lost. For this reason, the issue of whether a pure state
can evolve to a mixed state in the process of black hole formation and
evaporation is usually referred to as the "black hole information
paradox". [There are in fact two logically independent grounds for
the claim that the evolution of an initial pure state to a final mixed
state is in confict with quantum mechanics:
1. Such evolution is asserted to be incompatible with the fundamental
principles of quantum theory, which postulates a unitary time evolution
of a state vector in a Hilbert space.
2. Such evolution necessarily gives rise to violations of causality and/or
energy-momentum conservation and, if it occurred in the black hole formation
and evaporation process, there would be large violations of causality
and/or energy-momentum (via processes involving virtual black holes) in
ordinary laboratory physics.
Some advocate that a black hole cannot completely disappear but that
some of the original information persists as a kind of nugget. Others
believe that this information is re-emitted as some form of correlated
particles. Another view is that a new quantum theory of gravity will necessarily
be non unitary. Hawking has changed his original view that information
is lost and now advocate that the actual probability of sub atomic(and
virtual) black holes actually causing the loss of information is minuscule
and that unitarity is only violated in a mild sense. [He proposes that
in the presence of black holes, the quantum state of a system evolves
into a (non-pure state) density matrix --- a la von Neumann] This is somewhat
analogous to the improbable effect in the violation of the 2nd
law of thermodynamics or the approach to decoherence in QT. In effect
the sum over all the possible histories (geometries) of the universe,
results in the nullification of the non unitary effect of black holes
in the long term. Susskind on the other hand has applied t' Hooft's holographic
principle to sting theory and believes that the information is stored
in the horizon of a black hole [Indeed using string theory to calculate
the possible configurations of black holes has reproduced the BH formula
for its entropy -- as have LQG calculations]. This has been strengthened
more recently by Maldacinas conjecture (AdS/CFT correspondence), which
demonstrates that there is an equivalence between the string theory of
gravity in a 5D anti-de Sitter universe and the conformal supersymmetric
Yang- Mills theory on its horizon [This holographic duality becomes more
precise the larger the value of supersymmetry N]. Maldacina's conjecture
not only says that gravity is in some deep way the same as quantum field
theory but also implements the holographic principle in a concrete way.
Proof of Bekenstein Bound
Assume the contrary, that there is an entity 'A' such that the amount
of information needed to describe it, is much larger than its surface
area. Now 'A' cannot be a black hole because we know that the entropy
of a black holes that can fit inside 'A' must be equivalent to an area
less than that of 'A' but in this case its entropy must be lower than
the area of the screen in Planck units. If we assume that the entropy
of the black hole counts the number of its possible quantum states, this
is much less than the information contained in 'A'. Now 'A', according
to GR has less energy than a black hole that just fits inside 'A' and
so as we add energy to 'A' we reach a point at which it will collapse
into a black hole. However it now has an entropy which is equal to a quarter
of the area of 'A'. Since this is lower than the entropy of the original
'A' we have succeeded in lowering the entropy of a system, which contradicts
the second law of thermodynamics! Consequently if we accept the 2nd law
of thermodynamics we must believe that the most entropy that we can attribute
to 'A' is a quarter of its area
Bekenstein's law. With every horizon that forms a boundary separating
an observer from a region which is hidden from them, there is associated
an entropy which measures the amount of information which is hidden behind
it (and is proportional to the area of the horizon)
Unruh's law. Accelerating observers see themselves as embedded
in a gas of hot photons (Rindler particles) at a temperature proportional
to their acceleration. {As their acceleration increases they perceive
more virtual radiation. Now although this radiation is (non-locally) correlated,
their observable horizon shrinks. This is because light from a sufficientl
distant source can never catch up with a continually accelerating observer,
even though they can never reach the speed of light -- the greater the
acceleration the nearer is this horizon . Hence because much of their
world cannot be seen, this produces a randomness which implies an increased
temperature. This is in accordance with the principle of equivalence;
for both black holes and accelerating observers, the smaller the 'horizon'
the greater the random radiation (temperature). However in the case of
the former this area is the region into which information has fallen and
increases with entropy, while in the later, the visible region that surrounds
them reduces with increased acceleration, meaning that the universe of
information that is inaccessible increases. In both instances,
there is an increased temperature and decreased entropy, as the horizon
is reduced . . . deltaS = deltaQ/T }
* * * * * * * *
NB. . The entropy of a black hole is proportional to the area of its
event horizon and has an enormous value. [Entropy can be regarded as a
measure of how probability that system is to come about by chance] Now
because of the large black holes at the centres of galaxies, this black
hole entropy easily represents the major contribution to the entropy of
the known universe! Because of the second law of thermodynamics, the entropy
at the beginning of the universe must be very small. This beginning is
represented by the singularity of the big bang, which must be extraordinarily
special or fine tuned compared to the high entropy singularities that
lie at the centre of black holes. It therefore requires a new theory --
quantum gravity -- to explain the remarkable time asymmetry between the
singularities in black holes and that at the big bang.

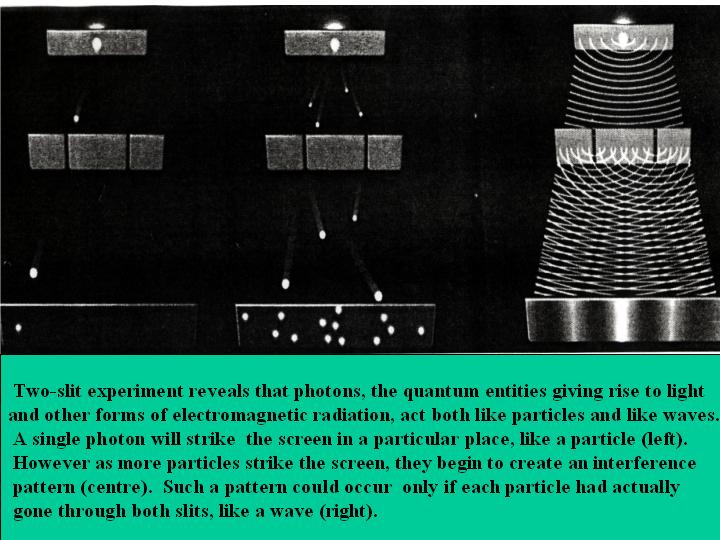
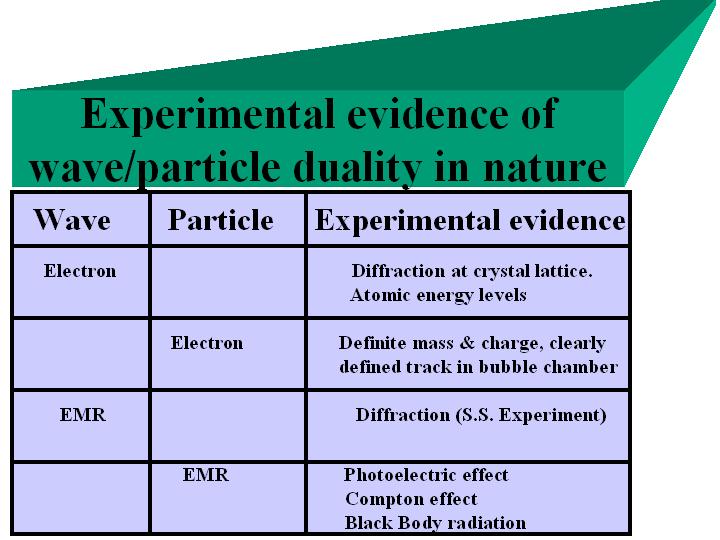
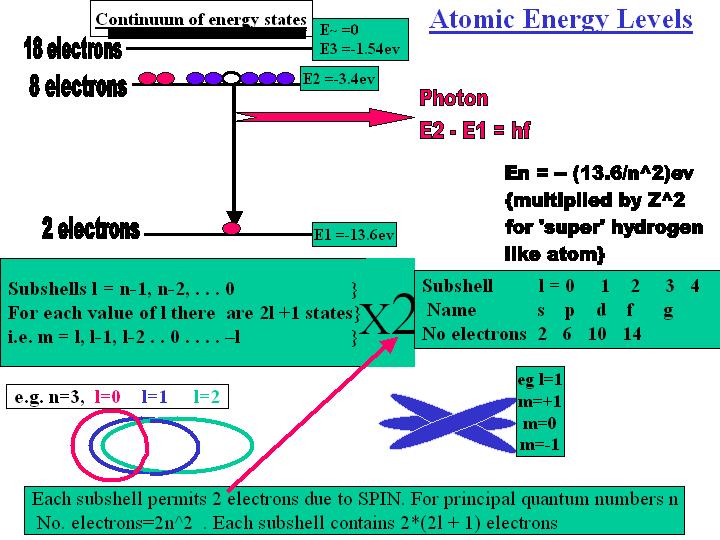
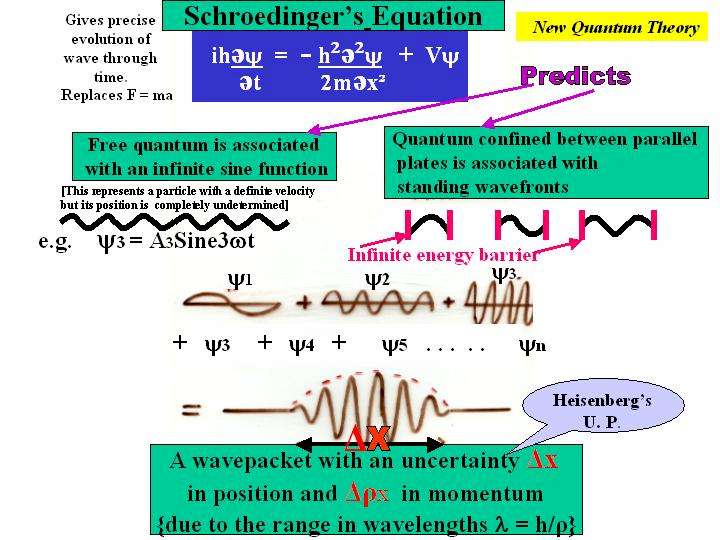
Fermions and Bosons;
The Janus of Quantum Theory
In Newtonian mechanics objects are described classically as particles
in which the position and momentum at a particular instant can be specified
exactly. A collection of particles in thermal equilibrium is described
in terms of Boltzmann statistics, in which particles are distinguishable.
In quantum mechanics a 'particle' is described by a wavefunction which
is acted upon by hermitian operators which extracts eigenvalues that represent
measurable observables. Such observables as momentum and position although
complimentary are also mutually exclusive (as enshrined by Heisenberg’s
uncertainty principle). A wavefunction does however have an ‘internal’
structure known as a spinor which is crucial in determining how the particle
behaves. A collection of such quanta is described either by Einstein-Bose
statistics (in the case of integer spin bosons) or by Fermi-Dirac statistics
(half odd-integer spin fermions), both of which involve ‘particles’
that are not distinguishable. It was in fact Dirac who first introduced
the concept of spinors into QT as a means of making Schroedingers equation
compatible with SR (such quanta obeyed the spin statistics of an assembly
of fermions).
Hence in QT all entities can be classified according to whether they
obey such fermionic statistics (with its anti-symmetric wavefunction)
or bosonic (symmetric) statistics. There is a whole lot of group theory
which shows that half-integer spins obey the former (e.g. those whose
angular momentum is 1/2h). This in turn means that 2 fermions cannot occupy
the same quantum state (Pauli’s Exclusion Principle), an important
fact since it explains the stability of the electron configurations in
an atom and hence allows the richness of the periodic table. Bosons on
the other hand like to be in the same quantum state and the fact that
they can be stimulated to do so is exploited by the 'Light Amplification
by Stimulated Emission of Radiation' (LASER). Super cooled helium-4 also
obeys these statistics (in this case bosons are conserved) and thus allows
the production of an Einstein-Bose condensate, the so- called fourth state
of matter (what ever happened to plasma?).Whole integer spinors (bosons)
faithfully represent the rotational group (they behave like the squares
in a Rubic cube) while fermions exhibit a non-faithful representation,
hence if you rotate an electron by one revolution it ends up being 'upside-down'.[
This property is responsible for its 'anti-social' behaviour, since it
gives rise to the anti-symmetric wavefunction that characterises an assembly
of fermions.]
Let us take another look at the origin of this double-headed aspect of
QT. A physical law needs to be invariant under rotation, hence we need
to know how to express a transformation, so as to maintain the symmetry
of an equation, with respect to all observers who are oriented in different
directions. Wavefunctions (state vectors) exist in Hilbert space which
involve complex numbers and undergo unitary transformations in
order that probabilities are conserved. The special unitary group SU(2)
achieves this and acts on the 2-dimensional space of spinors (so called
because it represents spin states). When the XYZ axes are rotated by an
angle @ (e.g. 360) the spinor rotates by only @ /2 (i.e.180). Hence we
have two important representations of the rotational groups viz. O(3)
acting on real vectors in Euclidean 3-D space and SU(2) acting on complex
space. The later is actually simpler (simply connected) while the latter
is doubly connected.
Wavefunctions must transform under this (compact) unitary group in order
to preserve transition amplitudes however relativity transformations involves
a non-compact Lie group. For simple rotational transformations this can
be achieved as already mentioned, by using a spinor representation,
which under the action of the Lorentz group, undergoes a unimodular
transformation and under the restriction to the rotational sub-group,
it also undergoes a unitary change. The Pauli matrices generate such a
special unitary group SU(2). Hence if an observer’s axes are rotated,
the group that transforms this wavefunction must be both unimodular
and unitary. This requires using spinor space not vector space
i.e. as vector co-ordinates go through an Euclidean rotation, the spinors
wavefunction evolves in a unitary manner.
This spinor space is not however a faithful representation of the rotational
group and leads to the result that 2 rotations are needed to make the
spinor function return to its original state and it is this which is the
cause of the Lande’ factor g = 2. [One rotation induces a negative
sign producing an anti-symmetric wavefunction, when two particles are
interchanged.] Although first rank spinors are a non-faithful representation
of the rotation group (e.g. electrons) as can be shown from studying unimodular
group space, higher rank spinors can produce faithful representations
e.g. photons. Pauli and Schwinger showed using the CPT theorem (the invariance
of physical laws under reversal of charge, parity and time), half integer
spinors have operators which are anti-symmetric i.e. fermions, while integer
spinors operators are bosonic. This can be achieved directly from the
group theory of higher rank spinors
Although not realising it at the time, Dirac was finding an equation
that allowed compatibility between the unitary group of QM and the unimodular
group of SR and it is this which produces g = 2, as well as invoking of
anti-matter and the necessity of a field theory. [Unfortunately as Cartan
has shown, such a spinor equation cannot be extended to the Riemannian
techniques required by GR.] Historically,
Dirac was motivated by the inadequacy of the Klein-Gordon equation. His
main dissatisfaction was not that this relativistic version of QT could
yield embarrassing negative values to the probability density, but rather
that it did not conform to his beloved transformation theory, which he
once remarked was his greatest single achievement. His contact transformations
showed that QT could be expressed using a variety of bases e.g. momentum
space. Just as GR was like a marble statue, which could be covered in
an endless variety of covariant space-time coordinates, so could the tenets
of QT be written in a countless choice of bases in Hilbert space.
The interchange of two non-distinguishable particles corresponds to 360
degrees of rotation in real space, which therefore corresponds to 180
degree of rotation of a (simple) spinor wavefunction. This does not affect
the probability of a wavefunction being made, since this depends on square
of the amplitude of the function, but it does change the sign of the wavefunction,
which means that it must be anti-symmetric. Such anti-symmetric wavefuctions
implies that no two quanta can occupy the same state i.e. Pauli’s
exclusion principle is invoked!
What about the symmetric function of bosons? Well they are also unitary
and unimodular, but the representation of the rotational group takes place
on a space, which is the product of two spinors, which faithfully represent
the rotational group. There is a great deal of group theory proving all
this and it can be shown that an odd number of spinors multiplied together
gives a non- faithful (fermionic) representation of the rotation group,
while an even number gives a faithful representation (bosons).
To recapitulate, only suitable way of representing QM, (whose wavefunction
evolves/transforms according to a unitary group) such that rotations of
the X,Y and Z axes, can be catered for, is to resort to spinor space.
The basic spinor rotates at half the rate as that of an Euclidean vector
and hence it has an angular momentum of ˝h and g = 2. This also causes
an interchange of particles (= 360 degrees of rotation) to give a sign
change, hence the function is antisymmetric, implying that no two particles
can occupy the same state (fermionic statistics). For bosons, the spinor
space is made up of an even number of spinors multiplied together (e.g.
2 for photons = spin 1h) and they faithfully represent the rotation group
and have symmetrical wavefunctions. Indeed an even number of fermions
may itself interacts with another of its ilk, in a bosonic fashion.
The more important group of transformations is the Lorentz group of special
relativity (involving boosts in velocity as well as rotations). There
is also a representation of this larger group in spinor space but although
it is unimodular it is not unitary and the spinor has 4 components described
by the transformation SU(2) * SU(2), (i.e. a pair of 2 spinors, each 2-spinor
being related by parity). Moreover SR forms a non-compact group, while
unitary transformations are compact and therefore SR is not compatible
with basic QT. There is a theorem that states that there is no finite
dimensional unitary representation of a non-compact Lie group and this
overtly prevents a unitary group from representing the full Lorentz
group. This leads to quantum field theory, which gets around the problem
by introducing "functionals"—spin functions with an infinite
degree of freedom. [For example Dirac’s equation in which there is
a ‘four spinor’ composed of a pair of ‘two spinors’
related by parity.] Supernumbers also allows a way around this problem
e.g. superstring theory.
Classically a particle has 3 degrees of freedom (X,Y & Z) while a
field has infinite degrees of freedom each position has a field value).
Quantum mechanically a particle (quanta) is represented by the
wave function which also has 3 degrees of freedom W(x,y,z). There is a
position operator and a momentum operator, which extracts eigenvalues
when acting on the wavefunction and these correspond to the classical
observables. For a (relativistic) field W(x,y,z) represents the
amplitude of probability of finding a given distribution of particles/antiparticles
of various energies and spin at that point (and takes the role of the
position operator in that of a particle Lagrangian). Whereas Quantum mechanics
allows the duality of particles and waves, quantum field theories allow
a duality between matter and energy, string theory allows a unification
of fermionic and bosonic fields. Remember that heisenberg's Uncertainty
Principle relates to the complementary uncertainties in a particles position
and momentum (~ rate of change of positioned) and when applied to fields,
it implies that the more we know about the value of a field (number of
particles at a location),.the less we know about its rate of change at
that location.
A spinor field transform unimodularly and this causes the wavefunction
(which has infinite degrees of freedom) to transform in the desired unitary
way. [The field, being a ‘functional’ behaves as if it is a
function with an infinite number of variables. It therefore avoids the
problem of there being no finite unitary representation of a non compact
group, such as the Lorentzgroup). This ensures that observable measurements
are in agreement with special relativity as well as QM. In Dirac’s
equation, no two spinors can occupy the same energy state (i.e. fermi
statistics), while for photons, the likelihood increases and their (bosonic)
statistics are expressed by the commutative relationships of the field
operators.
As already mentioned, it was the quest to find a relativistic wave equation,
which forced Dirac to introduce spinors as a necessity .[Cartan and later
van derWaerden developed a complete theory of spinor calculus. The discovery
of spinors came as something of a shock to the physics community, who
up until then had thought that tensors were the only possible representation
of the rotation group, while in actual fact if we relax the requirement
of being faithful, we can allow the two-valued representation
of spinors ]. This formulation also showed that particles had an inherent
spin of 1/2h (electrons become inverted when rotated by 360 degrees),
and the existence of anti-particles. [The prediction of anti particles,
however is an abandonment of the Dirac equation as a single particle equation,
since it is now required to describe both particles and antiparticles
and we must therefore view it as a field equation] The only way that a
spinor (which must obey a general unimodular transformation under a Lorentz
transformation), can conform to the unitary transformation demanded by
a quantum wave function, is if we move to what is sometimes referred to
as second quantisation, in which a many particle wave function is achieved
by changing the corresponding one particle wavefunction into a set of
operators satisfying certain commutational relations. This results in
a quantum field theory in which there is an indefinite number of particles
distributed throughout space i.e;
QM + SR = Quantum field theory
In Dirac's equation we have moved from a function to the concept of a
functional, which is a function with an infinite number of variables.
As in the concept of a field, every position in space and time is given
a variable value i.e we have infinite degrees of freedom. By considering
functionals of spin functions and assuming that that the Hilbert
space is a space of functionals, the spin can be extended so as to be
in agreement not only with the group of rotations but also with the full
Lorentz group! Under such a formalisation, when a Lorentz transformation
is applied all the spin functions will undergo a unimodular transformation
and hence behave like spinors, while spin functionals (the wave
function psi) will undergo a unitary transformation, as required in order
to preserve probability amplitudes. Dirac used his relativistic equation
to obtain a method of describing the interaction of electrons with their
electromagnetic field. This tentative way of doing electrodynamic calculations
involved incorporating into the Dirac action, the Maxwell field, which
although relativistic was not quantized (as was his electron field). This
approach therefore considered the Dirac electron interacting with a classical
Coulomb potential and although giving correct magnetic moment for the
electron (Lande factor g=2), does not account for more subtle refinements
such as the Lamb shift. There was already a way of expressing an electromagnetic
field as an assembly of bosons, by utilizing Fock space, constructed from
harmonic oscillators (together with the correct commutational relations
for its creation and annihilation operators). However this was not a relativistic
description of an assembly of photons. Later methods developed by Jordan,
Heisenberg and Wigner etc., involving the canonical approach, did however
produce a relativistic quantum field theory of electrodynamics. Alternatively,
there is Feynman's path integral method which relies on a concept that
was also initiated by Dirac. He elaborated it so as to incorporate interactions
with quanta of electromagnetic fields (photons) as well as virtual particles
and antiparticles of its own electron field. Quantum electrodynamics [QED],
does however suffer from embarrassing infinities which occur when probing
interactions at higher energies and these have to be removed by a process
known as renormalization (a technique that does not however work for quantum
gravity). Electrons however, are not the only source of electric charge
and a more complete description would allow for quarks! Such Quantum Flavour
and Colour Dynamics [QCD &QFD] that are incorporated in the Standard
Model, rely on gauge theories in which there is spontaneous symmetry breaking
that is crucial in explaining the mass of the gauge particles that carry
the interaction (and indeed possibly explain the fermionic masses in Grand
Unified Theories)
More generally, in order to quantize a classical field, we first express
it in a Lagrangian form and find its corresponding (position and momentum)
canonical conjugate variables -- the first of which I will denote as psi(x,t).
[The required classical equation for the field is then usually
retrieved by using Hamilton's equations]. Then we quantize the field by
subjecting the canonical field variables to the correct Heisenberg's commutational
relationships. The equation of motion for any quantum variable
'F' can then be obtained by replacing the Poisson bracket by the corresponding
Heisenberg commutator bracket (which can be found since F and the Hamiltonian
are given in terms of the known canonical variables). The quantum field
quantity psi(x,t) is then regarded as an Hermitian operator (rather than
a real numerical function) whose Fourier expansion can be written in terms
of its creation and anihilation operators and in a relativistic
field, we have to cater for both matter and ant-matter. These two operators
must also satisfy commutational relationships, depending on whether the
field represents an assembly of bosons or fermions.The quantity psi(x,t)
plays a role in field theory analagous to that played by x, the position
vector in particle (quantum) mechanics and the two canonical variables
obey the same commutational rules of Heisenberg. The process of regarding
ps(x,t)i as an operator rather than a number, is therefore part and parcel
of the process of second quantization (i.e. the quantization of a field.)
This field quantization has an obvious interpretation as a many particle
theory, where the square of the amplitude is proportional to the number
of particles present. An alternatively method of providing a quantum field
theory, is to apply the path integral method and use Feynman propagators
( which are the inverse of the operator appearing in the quadratic part
of the Lagrangian), to determine the contribution of each of the scattering
probabilities of the particles interacting with their field.
Supersymmetry involves combining fermions (the basic constituents of
matter) and bosons (responsible for the fundamental forces) on an equal
footing in the same quantum field theory. As well as unifing fermions
with bosons, it also unifies spacetime symmetries with internal symmetries,
and (in the case of local supersymmetry), gravity with matter. The non
compact groups of SR do not have a unitary representation in commuting
numbers (e.g complex or real space) but there is a possibility in superspace.
Bosons arise naturally as a field which provides the interaction between
fermion particles, which usually manifest as a force (electromagnetism,
strong nuclear interaction and gravity). Different fermions (e.g. electrons,
neutrons) can be represented as an internal state, in which these components
(fermions) are symmetric under certain local gauge transformations. [This
state behaves like spinors and the gauges like SU(2)]. However the boson
field associated with gravity (gravitons of spin 2h), must belong to the
none compact group of SR, since GR which describes gravity, is a localised
(hence generalised) form of SR. As mentioned above, we therefore need
to resort to anti-commuting numbers in order to achieve this master supersymmetry
and obtain unification. Fermions and bosons are therefore united in the
same Quantum field theory and can be interchanged into each others state
by symmetrical internal transformations e.g. electrons-sleptons or gravitons-
gravitinos. Supersymmetry is an extension of ordinary Poincare space-time
symmetry which is obtained by adjoining N spinorial generators whose anticommutator
yields a translation generator (hence producing gravity when localized).
This symmetry can be realized on ordinary fields (functions of space-time)
by transformations that mix bosons and fermions but a more compact alternative
to this component field approach is given by the superspace- superfield
approach. Here superspace is an extension of ordinary space-time so as
to include extra anticommuting coordinates in the form of N two component
Weyl spinors $. Superfields Psi(£$) are then functions defined over
this space. The transformations mixing bosons and fermions are then constant
translations of the $ coordinate and also related rotations of the $ into
the space-time coordinate £
In (closed) superstring theory, upon quantization, the canonical conjugate
operators decompose into a Fourier series, which contain left and right
handed harmonic oscillators which do not interact (that is as the string
propagates, it has distinct right and left moving oscillator modes). Quanta
are therefore represented by the dynamics of strings and different vibrational
modes in different bosonic/ fermionic coordinates represent different
quanta. The left moving modes are purely bosonic and exist in a 26 dimensional
space, which has been compactified to 10 dimensions. The right moving
modes only live in this 10 dimensional space and contain the supersymmetric
part of the theory, this requires the introduction of superpartners that
differ by a spin half (e.g. electron-slepton, photon-photino, etc) as
well as the graviton/gravitino. The compactified 16 dimensional string
lives on the root lattice space (e.g. 16D Tori), of an E8*E8 isospin (internal)
symmetry, which is more than large enough to contain the required spectum
of particles. When the left moving half and the right moving half are
put together they produce the heterotic string (meaning "hybrid vigour").
Compactification of the extra six dimensions on a Ricci flat (e.g Calabi-Yau)
manifold, then reduces the 10 dimensional superstring into our familiar
4 dimensional space-time, breaking the E8*E8 symmetry to produce the electroweak
and strong interactions that are represented by U(1), SU(2) and SU(3)
gauge symmetries. [ Under compactification that produces the Calabi-Yau
space, one of the E8 groups is broken down to its E6 subgroup and E6 is
a good candidate for a Grand Unified Theory, as it contains the subgroups
of the Standard Model. The other E8 sector would describe (shadow) matter
that could (only) interact gravitationally with the 'E6 matter']
Hence although the reason that fermions and bosons exist in subtle, deep
and complex, if these symmetries were not enforced upon nature, we would
not have the richness that we observe in the universe. This is nowhere
more evident than in the creation of our own planet Earth and in the very
laws that are responsible for its existence.
Regarding superunification it is not possible to satisfactorily incorporate
gravity (which is governed by the non-compact Poincare group) in what
is known as a Unitary representation (that dictates the other 3
quantum interactions), unless one resorts to supernumbers, which combines
both fermions and bosons via supersymmetry. This concept was originally
invoked in the early study of string theory but although this has received
a recent surge in popularity, supersymmetry itself does not require a
string formulation. I'll let Dirac have the last (controversial) word
"Physical laws should have mathematical beauty" (epitaph)
* * * * * * * * * * * * * * *
ADDENDUM
Below is a summary of the 5 versions of String Theory
Preamble
String theory can trace its origins from a study of S-matrix theory (S
for scattering), which was initiated by Heisenberg and championed by John
Wheeler and later Geoffrey Chew. This approach allows the description
of quantum interactions in terms of inputs and outputs, without a detailed
knowledge of what was actually occurring 'In the black box' but merely
relying upon certain constraints of relativity symmetry and quantum theory
etc. Gell-Mann had noticed regularities, so called T dualities (symmetries)
present in these S-matrix approaches and this was later consolidated by
Veneziano when he discovered that it obeyed the Euler beta function. Still
at this stage no one knew what was the mechanism behind these scattering
diagrams and understanding such a mechanism was crucial to understanding
the strong force which dominated such collisions and the ever increasing
plethora of newly discovered particles (this was before the advent of
QCD and quarks). It was however later discovered by Nambu, Susskind et
al, that the mechanism could be explained by resorting to a string rather
than the ubiquitous particle description (of the Lagrangian). This Bosonic
strings was found to require 26 dimensions in order for the theory to
obey the requirements of special relativity. However such a string theory
was employed to describe the hadrons which were predominantly fermions.
In 1971 Ramond found that by employing spinors, he could derive a string
theory for fermions in 2 dimensions and in doing so, discovered an early
form of supersymmetry [SUSY]. [Supersymmetry was originally used in an
attempt to produce a Master group, that would allow both internal (isospin)
groups and noncompact space-time groups to be combined in a non-trivial
fashion Mandula and Coleman had proved that the Poincare group of translations,
rotations and boosts is the maximal symmetries applicable to space-time
but this did not take into account the possibility of supermanifolds].
however Ramonds superstring theory had only one dimension of space and
one of time but in 1973 Wess and Zumino developed a 4 dimensional supersymmetric
(particle) theory. Then in 1976 this theory was extended so as to include
gravity - - -producing supergravity! [Basically since their spins are
different, bosons and fermions transform differently when they rotate
in space. Supersymmetry transformations must involve space and time in
order to compensate for this distinction. In actual fact a local supersymmetric
transformation (as decreed by SR), requires a localised transformation
in space-time, that is inherent in Einstein’s General Relativity
theory of gravity.]
Although Ramonds strings implied the possible appearance of bosons (by
the joining up of 2 fermionic strings), it was Schwarz, Scherk and Neveu
who were the first to formulate an explicitly fermioni/boson string .
With this new 'spinning string theory' (which could take account of hadrons
as being fermions), Schwarz and Scherk were able to produce a supersymmetric
version that removed the embarrassing tachyons (imaginary mass/faster
than light, particles), that were present in the purely bosonic string.
They also showed that the number of required dimensions could be reduced
to just 10 and by reducing the size of the string by a factor of 20 they
invoked an extra massless spin 2 particle, (which they later realised
had properties similar to the graviton, also predicted in supergravity.)
In any other number of dimensions, unaccepttable vibrational modes of
the string give rise to nonsesical negative probabilities. Also note that
in particle theory gravity interacts too stongly giving infinite values
at high eneregies, whereas string theory softens their interaction and
supersymmetry cancancel many of these divergent effects
By 1974 string theory entered a dry period which, saw the success of
quantum chromodynamics in explaining new strong interaction phenomena.
What followed was the rise of the standard model and later supergravity,
which were considered more compelling theories and retained the more familiar
particle viewpoint. Interest in superstring theory underwent a revival
when in 1984 Schwarz and Green showed that certain unwanted terms that
led to anomalies (these are symmetry violations such as the conservation
of energy), miraculously canceled. These symmetries must be exact otherwise
there is no way to eliminate the unwanted polarization of the gauge boson.
For example, the photon only allows 2 transverse polarizations and the
unwanted longitudinal direction is forbidden by internal symmetries -
- - simmilar internal symmetries restrict the W, Z and gluon gauge bosons.
[Group theory of Wigner et al, shows that massles particles only have
2 polarizations, while massive gauge bosons have 3. This is because massless
particles travel at the speed of light and are therefore never at rest.
Consequently they single out a particular direction of motion and hence
distinguish the perpendicular motion from the remaining polarization along
the direction of travel. It turns out that for massless gauge bosons,
physical polarization oscillate only in the 2 perpendicular directions.]
Hence Schwarz and Green showed that the sum of the quantum mechanical
contributions to all these possible symmetry breaking anomalies
in 10D superstring theory is zero Also by radically reducing the size
of the string, they could make a leap forward in unification by identifying
the spin 2 boson as the graviton. Superstring theory also received a boost
from the work of Witten, who produced several new results, such as the
identification of Calabi-Yau spaces as candidates for the extra curled
up dimensions and the dependence of the number of generations of particle
to the Euler number. [The precise size and shape of the extra dimensions
has a profound effect on string vibrational patterns and hence on particle
properties. Calabi-Yau spaces produced the left handed chirality that
is needed to explain weak interactions which violate parity by distinguishing
between left and right handed interactions.Furthermore, rolling up the
extra dimensions into a Calabi-Yau manifold preserves supersymmetry by
just the right amount; too little prevents supergravity, too much and
we wouldn't get left handed particles that had different interactions
from the right handed ones]]
One of the appeals of superstring theory is that it overcomes the conflict
of QT with GR since it smears out space time in a way that causes the
microcosm to come to an end near the Plank scale and so obviates the embarrassing
infinities that had plagued other methods. Also, all the fundamental quanta
( both particles and their messengers) can be explained as various vibrations
of the same string theory. Also if a huge collection of strings all vibrate
in just the right coordinated way throughout all of space, they can provide
a uniform background that is similar to the Higgs ocean and these effects
should be calculable as opposed to imputed as in previous particle
versions [Note that only the zero mode of a string can be associated with
the known particles, since the first excitation of a string has a mass
equal to that of the Plank mass (and multiples thereof for higher harmonic
vibrations), which is far too large to be created in particle accelerators.
These zero mode vibrations would then have to pick up masses by a Higgs
mechanism, so as to produce the observed spectrum of fermions etc.]. String
vibrations that initially yielded zero mass, would then acquire tiny nonzero
masses through the drag force they experience as they move and vibrate
through the string version of the Higgs ocean. In actual fact supersymmetry
helps solve the Hierarchy problem since it allows a light Higgs
particle when there are large quantum contributions to its mass from virtual
particles. (These contributions would otherwise require a 'fudge factor'
which needs to be continually finely tuned at each energy scale). with
SUSY the contributions from both partner and superpartner cancell out
(fermion contribution is negative while bosons is positive). Supersymmetry
also ensures that the various strengths of the interactions converge to
a common value at a high enough energy, a feature that is necessary for
unification but is inexact in other GUTs.
However it transpired that there could be 5 variations of 'string theory'
and that each of them was strongly effected by the topology of the manifold.
Although the orbifolds/Calabi-Yau was the most likely, this allowed many
thousands of possibilities without much guiding principles as to how to
proceed. The prompted the next revolution in string theory M-THEORY, in
which all 5 versions of string theory are seen as different perspectives
of a higher 11 dimensional Brane theory. [Note that string theory is pertubative
since it requires the breaking apart interaction and reforming of strings,
whereas M-theory is non pertubative]. Witten was able to show that the
approximate (pertubative) string theory equations that are written in
10 dimensions, were actually 5 approximate descriptions of a single underlying
11 dimensional theory. This whole enterprise has therefore lead to a revolution
in geometry, comparable to the that of Gauss and Riemann's transformation
of the Euclidean geometry that had dominated for 2 Millennia. In addition
to considering microscopic p-branes, more recent developments have lead
to theories involving D-Branes (which could contain strings wholly within
them or alternatively just restrain their ends) and macroscopic Brane
Worlds (with or without strings).
Technicalities
Up to now, String Theory is only well understood at the perturbative
level. The field theory diagrams are replaced
by two dimensional Riemann surfaces, with the loop expansion being performed
by an expansion in the genus of the surfaces. It is a formulation of first
quantization, where the path integral is weighed by the area of the Riemann
surface and the external states are included by the insertion of the appropriate
vertex operators The perturbative string coupling constant is determined
by the vacuum expectation value of a massless real scalar field, called
the dilaton, through the relation gs = exp(s). The thickening of Feynman
diagrams into ‘surface’ diagrams improves considerably the ultraviolet
behavior of the theory. String Theory is ultraviolet finite.
Lorentz invariance on the target space or conformal invariance on the
worldsheet fixes the number of spacetime dimensions (twentysix for bosonic
strings and ten for superstrings). As our low energy world is four dimensional,
String Theory incorporates the Kaluza-Klein idea in a natural way. The
effect of a non-zero finite radius R for the compactified dimension is
just a tower of Kaluza- Klein states with masses n/R. But in String Theory,
the string can wind m times around the compact dimension. This process
gives a contribution to the momentum of the string proportional to the
compact radius, mR/a'. These quantum states become light for R --- = 0.
The dimensional reduction of a String Theory in D dimensions is another
String Theory in D dimensions. This is T duality which is discussed below.
*!* [Under spacetime compactifications, the
type IIA and
the type IIB string theories are unified by the T -duality symmetry. It
is an exact symmetry of the theory already at the perturbative level and
maps a type IIA string with a compact dimension of radius R to a type
IIB string with radius a'/R.] The heterotic string is constructed from
a right moving closed superstring and a left-moving closed bosonic string.
Conformal anomaly cancellation demands twenty-six bosonic target space
coordinates in the left-moving sector. The additional sixteen left-moving
coordinates XI L, I = 1, ..., 16, are compactified on a T 16 torus, defined
by a sixteen-dimensional lattice, �16, with some basis vectors {eI i },
i = 1, ..., 16. The left-moving momenta pI live on the dual lattice �16.
There is also a T -duality symmetry relating the two heterotic strings.
viz. SO(32) and E8 × E8.
For the bosonic string, the lowest vibrating mode correponds to a tachyon
(a 'faster than light' particle with an imaginary mass). It indicates
that we are performing perturbation theory arround an unestable minimum.
Supersymmetry gives a very economical solution to this problem.
In a supersymmetric theory the Hamiltonian operator is positive semi-definite
and the ground state has always zero energy. It is also very appealing
from the point of view of the cosmological constant problem. Furthermore,
supersymmetry also introduces fermionic degrees of freedom in the physical
spectrum. [Superspace is obtained by adding {four} spinor degrees of freedom
to the spacetime coordinates xµ.]
As already mentioned, another important consequence of string theory,
is the prediction on the number of dimensions of the target space where
the perturbative string propagates. Lorentz invariance on the target space
or conformal invariance on the worldsheet fixes the number of spacetime
dimensions (twenty six for bosonic strings and ten for superstrings).
As our low energy world is four dimensional, String Theory incorporates
the Kaluza-Klein idea in a natural way. But again the one-dimensional
nature of the string gives a quite di�erent behavior of String Theory
with respect to field theory. The dimensional reduction of a field theory
in D spacetime dimensions is another field theory in D-1 dimensions. The
effect of a non-zero finite radius R for the compactified dimension is
just a tower of Kaluza- Klein states with masses n/R. But in String Theory,
the string can wind m times around the compact dimension. This process
gives a contribution to the momentum of the string proportional to the
compact radius, mR/a'. These quantum states become light for R approaching.
zero. The dimensional reduction of a String Theory in D dimensions is
another String Theory in D dimensions. This is T duality*!*
The final important consequence comes from the cancellation of spacetime
anomalies (gauge, gravitational and mixed anomalies). It gives only the
following five anomaly-free superstring theories in ten spacetime dimensions.
Type I SO(32):
This is a theory which contains unoriented open and closed superstrings.
It has one (N=1) supersymmetry in 10 dimensions. Open strings can carry
gauge degrees of freedom at their endpoints, and cancellation of anomalies
uniquely constrains the gauge group to be SO(32). It contains D-branes
with 1, 5, and 9 spatial dimensions.
Type IIA:
This is a theory of closed superstrings which has two (N=2) supersymmetries
in ten dimensions. The two gravitini
(superpartners to the graviton) move in opposite directions on the closed
string world sheet and have opposite
chiralities under the 10 dimensional Lorentz group, so this is a non-chiral
theory. There is no gauge group. It contains
D-branes with 0, 2, 4, 6, and 8 spatial dimensions.
Type IIB:
This is also another closed superstring theory with N=2 supersymmetry.
However in this case the two gravitini have the
same chiralities under the 10 dimensional Lorentz group, so this is a
chiral theory. Again there is no gauge group, but
it contains D-branes with -1, 1, 3, 5, and 7 spatial dimensions.
The SO(32) and E8 × E8 heterotic strings.
The heterotic string is constructed from a right moving closed superstring
and a left-moving closed bosonic string. Conformal anomaly cancellation
demands twenty-six bosonic target space coordinates in the left-moving
sector. The additional sixteen left-moving coordinates XI L, I = 1, ...,
16, are compactified on a T 16 torus, defined by a sixteen-dimensional
lattice, �16, with some basis vectors {eI i }, i = 1, ..., 16. The left-moving
momenta pI L live on the dual lattice e�16. . The modular invariance of
the one-loop diagrams restricts the lattice to be self-dual (e�16 = �16).
There are only two even self-dual sixteen-dimensional lattices. They correspond
to the root lattices of the Lie groups SO(32)/Z2 and E8 × E8.
SO(32) Heterotic:
This is a closed string theory with worldsheet fields moving in one direction
on the world sheet which have a
supersymmetry and fields moving in the opposite direction which have no
supersymmetry. The result is N=1
supersymmetry in 10 dimensions. The non-supersymmetric fields contribute
massless vector bosons to the spectrum
which by anomaly cancellation are required to have an SO(32) gauge symmetry.
E8 x E8 Heterotic:
This theory is identical to the SO(32) Heterotic string, except that the
gauge group is E8 X E8 which is the only other
gauge group allowed by anomaly cancellation.
We see that the Heterotic theories don't contain D-branes. They do however
contain a fivebrane soliton which is not a
D-brane. The IIA and IIB theories also contain this fivebrane soliton
in addition to the D-branes. This fivebrane is usually
called the "Neveu-Schwarz fivebrane" or "NS fivebrane".
It is worthwhile to note that the E8 x E8 Heterotic string has historically
been considered to be the most promising string
theory for describing the physics beyond the Standard Model.. This is
because the SU(3) x SU(2) x U(1) gauge group of the standard model can
fit quite nicely within one of the E8 gauge groups. The matter under the
other E8 would not interact except through gravity, and might provide
a answer to the Dark Matter problem in astrophysics. Due to our lack of
a full understanding of string theory, answers to questions such as how
is supersymmetry broken and why are there only3 generations of particles
in the Standard Model have remained unanswered. Most of these questions
are related to the issue of compactification .
"Gravity exists, so if there is any truth to supersymmetry then
any realistic supersymmetry theory must eventually be enlarged to a supersymmetric
theory of matter and gravitation, known as supergravity. Supersymmetry
without supergravity is not an option, though it may be a good approximation
at energies below the Planck Scale. Supergravity is itself only an effective
nonrenormalizable theory which breaks down at the Planck energies. So
if there is any truth to supersymmetry then any realistic theory must
eventually be enlarged to superstrings which are ultraviolet finite. Supersymmetry
without superstrings is not an option. Superstring theory is itself only
a perturbative theory which breaks down at strong coupling. So if there
is any truth to supersymmetry then any realistic theory must eventually
be enlarged to the non-perturbative M-theory, a theory involving higher
dimensional extended objects: the super p-branes. Supersymmetry without
M-theory is not an option." . . . . . . . S. Weinberg
The following results helped enthuse the superstring revolution
1) Green and Schwarz discovered that the gravitational and Yang- Mills
anomalies of the ten-dimensional superstrings all cancel provided the
gauge group is either SO(32) or E8 � E8;
2) Gross, Harvey, Martinec and Rohm discovered the heterotic (hybrid)
string with the above gauge groups;
3) Candelas, Horowitz, Strominger and Witten discovered that the E8 �
E8 heterotic string admits spontaneous compactifciation to four dimensions
on a six-dimensional Calabi-Yau manifold. The resulting four dimensional
theory resembles a GUT theory based on the group E6. In particular, there
are chiral families of quarks and leptons.
Schematically
we can summarise heterotic string theory as follows
The simplest solution is of course 26D flat spacetime with constant values
of all the fields. For this case we have a 2D free
theory, which can be easily quantized by solving the wave equation , the
fields can be written as:
(1) . . . . . . .Xm(u,v) = Xm,r(u-v) + Xm,l(u+v)
as usual,Xm,r and Xm,l represent right- and left-moving modes of the string
respectively, with an harmonic Fourier mode expansion
Since this is a free theory, quantization assigns canonical commutation
relations to the Fourier coefficients like the
oscillators of the harmonic oscillator. The Hamiltonian then gives rise
to the mass formula:
(2) . . . . . . . . . . M^2 = N,r + N,l - 2
Where N,r + N,l refer to the harmonic oscillator occupation numbers for
left and right movers and the level matching condition
requires N,r =N,l for consistency. Note that the `vacuum' state ( N,r
= N,l = 0) is a tachyon and the next state requires
one left-moving and one right-moving oscillator ( N,r =N,l =1), since
both oscillators carry a target space index, the state
corresponds to an arbitrary two-index tensor of which the symmetric part
is the metric Gmn, the antisymmetric
part is and the trace is the dilaton phi.
The instability due to the tachyon can be easily cured by supersymmetrizing
the theory. In that case the tachyon state is
projected out. The most popular supersymmetric string theory is the heterotic
string. In this theory, only the right moving
modes have a fermionic partner and consistency requires that they live
in a 10D space rather than the 26D space of the
bosonic string. The left moving modes however are purely bosonic, but
the 26D space of these modes is such that the extra
16 coordinates are toroidally compactified, giving rise to extra massless
states, which in this case are vector-like, as we will
see next, and correspond to the gauge fields of SO(32) or E8 xE8.
In order to construct string models in less than 10D as well as to understand
the heterotic string construction, we need to consider the simplest compactifications
which correspond to the extra dimensions being circles and their higher
dimensional generalization. Let us first see the case of a circle S1 This
means that the 10D space is represented by flat 9D spacetime times a circle
S1. We know that a circle is just the real line identifying all the numbers
differing by 2PiR, where R is the radius of the circle. So the only difference
with the flat space discussed above are the boundary conditions. The solution
of the wave equations are now as in (2). But now Pr = m/2R - nR and Pl
= m/2R +nR, . m is an integer reflecting the fact that the momentum in
the compact direction has to be quantized in order to get single-valued
wave function. The integer n however refers to the fact that the string
can wind around several times in the compact dimension and is thus named
the `winding number'. The mass formula is then:
(3) . . . . . . . . . M^2 = Nr + Nl - 2 + m^24R^2 +n^2R^2 . . . . .
. . . . . . Nr - Nl = mn
This shows several interesting facts. First, for n =0 and varying m, we
obtain an infinite tower of massive states with
masses ~1/R; these are the standard `momentum states' of Kaluza-Klein
compactifications in field theory. In particular the
massless states with n=m=0 and one oscillator in the compact direction
are vector fields in the extra dimensions giving
rise to a U(1)l X U(1)r Kaluza-Klein gauge symmetry. The states with n
/= are the winding states and are purely stringy; they represent string
states winding around the circle, they have mass ~R. Second, there are
special values of and which can give rise to extra massless states. In
particular for n=m=+-1 we can see that at the special radius R^2=1/2 in
units of alpha' , there are massless states with a single oscillator Nr=1,
Nl=0 corresponding to massless vectors which in this case generate SU(2)l
X SU(2)r. This means that the special point in the `moduli space' of the
circle R^2=1/2 is a point of enhanced symmetry. The original U(1)l X U(1)r
Kaluza-Klein symmetry of compactification on a circle gets enhanced to
SU(2)l X SU(2)r. This is a very stringy effect because it depends crucially
on the existence of winding modes (n/=0). The third interesting fact about
this compactification is that the spectrum is invariant under the following
`duality' transformations :
(4) , , , , , , , R<-> 1/2R . . . . .m <->n
This is also a stringy property. It exchanges small with large distances
but at the same time it exchanges momentum
(Kaluza-Klein) states with winding states. This symmetry can be shown
to hold not only for the spectrum but also for the
interactions and therefore it is an exact symmetry of string perturbation
theory. Unfortunately, constructing 4D superstring models from circle
and toroidal compactifications results in N=4 supersymmetry and therefore
they are not interesting for phenomenology, because they are not chiral.
To obtain a chiral model we should construct models with at most N=1 supersymmetry,
hence the need to examine orbifold or more generally, Calabi-Yau manifolds.
The five superstring theories appear to be very different when viewed
in terms of their descriptions in weakly coupled
perturbation theory. In fact they are all related to each other by various
string dualities. We say two theories are dual when
they both describe the same physics. The first kind of duality that we
will discuss is called T-duality. This duality relates a theory which
is compactified on a circle with radius R, to another theory compactified
on a circle with radius 1/R. Therefore when one theory has a dimension
curled up into a small circle, the other theory has a dimension which
is on a very large circle (it is barely compactified at all) but they
both describe the same physics! The Type IIA and Type IIB superstring
theories are related by T-duality and the SO(32) Heterotic and E8 x E8
Heterotic theories are also related by T-duality.
The next duality that we will consider is called S-duality. Simply put,
this duality relates the strong coupling limit of one theory
to the weak coupling limit of another theory. (Note that the weak coupling
descriptions of both theories can be quite different
though.) For example the SO(32) Heterotic string and the Type I string
theories are S-dual in 10 dimensions. These means
that the strong coupling limit of the SO(32) Heterotic string is the weakly
coupled Type I string and visa versa. One way to
find evidence for a duality between strong and weak coupling is to compare
the spectrum of light states in each picture and
see if they agree. For example the Type I string theory has a D-string
state that is heavy at weak coupling, but light at strong
coupling. This D-string carries the same light fields as the worldsheet
of the SO(32) Heterotic string, so when the Type I
theory is very strongly coupled this D-string is becomes very light and
we see the weakly coupled Heterotic string description
emerging. The other S-duality in 10 dimensions is the self duality of
the IIB string: the strong coupling limit of the IIB string is
another weakly coupled IIB string theory. The IIB theory also has a D-string
(with more supersymmetry than the Type I
D-string and hence different physics) which becomes a light state at strong
coupling, but this D-string looks like another
fundamental Type IIB string.
T Duality *!*
A symmetry whereby a string theory compactified on a small circle and
a string theory compactified on a large circle give rise to identical
physics. The basic idea of T duality (T for turns) can be illustrated
by considering a compact dimension consisting of a circle of radius R.
In this case there are two kinds of excitations to consider. The first,
which is not special to string theory, are Kaluza--Klein momentum excitations
on the circle, which contribute (n/R)2 to the energy squared, where n
is an integer. Second there are winding-mode excitations, due to a closed
string winding m times around the circular dimension, these are special
to string
theory. If
. . . . T =Lst^2/2Pi
denotes the string tension (energy per unit length), the contribution
to the energy squared is
Em=2pmRT.
T duality exchanges these two kinds of excitations by exchanging m with
n and
. . . . R <-> Lst ^2/R
This is part of an exact map between a T-dual pair A and B. Hence T-duality
states that nothing changes if we interchange the roles of the Kaluza-Klein
and winding particles providing we also exchange the radius of the circle
R by its inverse 1/R.
One implication is that usual geometric concepts break down at short distances,
and classical geometry is replaced by "quantum geometry," which
is described mathematically by 2D conformal field theory. It also suggests
a generalization of the Heisenberg uncertainty principle according to
which the best possible spatial resolution Dx is bounded below not only
by the reciprocal of the momentum spread, Dp, but also by the string scale
Lst. (Including non-perturbative effects, it may be possible to do a little
better and reach the Planck scale.)
Two important examples of superstring theories that are T-dual when compactified
on a circle are the IIA and IIB theories and the HE and HO theories. These
two dualities reduce the number of distinct theories from five to three.
S Duality
A symmetry whereby a string theory with a large coupling constant and
a string theory with a small coupling constant give rise to identical
physics. Suppose now that a pair of theories A and B are S-dual. This
means that if f denotes any physical observable and £ denotes
the coupling constant, then;
. . . fA(£) = fB(1/£)
(The expansion parameter a introduced earlier corresponds to £)
This duality, whose recognition was the first step in the current revolution,
generalizes the electric-magnetic symmetry of Maxwell theory. Since the
Dirac quantization condition implies that the basic unit of magnetic charge
is inversely proportional to the unit of electric charge, their interchange
amounts to an inversion of the charge (which is the coupling constant).
So S-duality (S for strong -weak), allows the roles of the Noether (electric)
charge and the topological (Bianchi) charge (magnetic monopole) to be
reversed. Therefore if we have an electric charge of quantised value me
and a magnetic charge of value n/e (to be consistent with Dirac's
theory), then S-Duality states that if we change the integers m
and n, we must also exchange e with 1/e and go from
a regime of weak coupling to a regime of strong coupling! [It can also
be shown that in M-Theory, the electric charge of the fundamental string
and the magnetic charge of the solitonic fivebrane obey a Dirac quantization
rule. The fivebrane is the `magnetic' dual of the `electric' membrane
in D=11, in agreement with the general formula that the dual of a p-brane
is a ~p-brane with ~p = D-p-4 .For each (p+1)-form in the Lagrangian there
is an associated electric-type p-brane solution and a magnetic-type (6
-p) brane solution, carrying Qp and Q(6-p) charges respectively.
S duality relates the type I theory to the HO theory and the IIB theory
to itself. This explains the strong coupling behavior of those three theories.
In type IIB string theory, when the value of its dilaton (a scalar field
that determines the size of the coupling constant), is changed from a
positive to a negative value, the 2 theories are identical.There is therefore
a duality under the exchange of a large coupling constant to a small coupling
constant.
The understanding of how the IIA and HE theories behave at strong coupling,
which is by now well-established, came as quite a surprise. In each of
these cases there is an 11th dimension that becomes large at strong coupling,
the scaling law being
. . . . . L11 = £^2/3
In the IIA case the 11th dimension is a circle, whereas in the HE case
it is a line interval (so that the eleven-dimensional space-time has two
ten-dimensional boundaries). The strong coupling limit of either of these
theories gives an 11-dimensional
space-time. The eleven-dimensional description of the underlying theory
is called "M theory." As yet, it is less well understood than
the five 10-dimensional string theories. [There are many additional dualities
that arise when more dimensions are compactified]
T-duality transforms electrically charged winding states into electrically
charged Kaluza-Klein states, but S-duality transforms elementary electrically
charged string states into solitonic monopole and dyon states (dyons carry
both electric and magnetic charge).
T and S duality can be combined under a so called U-Dualty
Mirror Symmetry
This applies when trhe 6 dimensions are rolled up into 2 different Calabi-Yau
manifolds, yet the resulting 4D space-time long distance theory can be
the same The mirror manifold of a given Calabi-Yau space could be entirely
different in shape size twisting or genus
D-Branes
What about the nonperturbative effects in String Theory?. Does String
Theory incorporate nonperturbative excitations (string solitons)?. Are
there also strong-weak coupling duality transformations in String Theory?.
Before the role of D-branes in String Theory were appreciated, the answers
to these three questions were not clear. For instance, it was known, by
the study of large orders of string perturbation theory, that the nonperturbative
effects in string theory had to be stronger than in field
theory, in the sense of being of the order of exp(-1/gs) instead of order
exp(-1/g2 s) , but it was not known which were the nature of such nonperturbative
effects. With respect the existence of nonperturbative objects, the unique
evidence came form solitonic solutions of the supergravity equations of
motion which are the low energy limits of string theories. These objects
were in general extended membranes in p + 1 dimensions, called p-branes.
Another source of insight into non-perturbative properties of superstring
theory has arisen from the study of a special class of p-branes called
Dirichlet p-branes (or D-branes for short). The name derives from the
boundary conditions assigned to the ends of open strings. The usual open
strings of the type I theory satisfy a condition (Neumann boundary condition)
that ensures that no momentum flows on or of the end of a string. However,
T duality implies the existence of dual open strings with specified positions
(Dirichlet boundary conditions) in the dimensions that are T-transformed.
More generally, in type II theories, one can consider open strings with
specified positions for the endpoints in some of the dimensions, which
implies that they are forced to end on a preferred surface. At first sight
this appears to break the relativistic invariance of the theory, which
is paradoxical. The resolution of the paradox is that strings end on a
p-dimensional dynamical object -- a D-brane. D-branes had been studied
for a number of years, but their significance was explained only recently.
The importance of D-branes stems from the fact that they make it possible
to study the excitations of the brane using the renormalizable 2D quantum
field theory of the open string instead of the non-renormalizable world-volume
theory of the D-brane itself. In this way it becomes possible to compute
non-perturbative phenomena using perturbative methods. Many (but not all)
of the previously identified p-branes are D-branes. Others are related
to D-branes by duality symmetries, so that they can also be brought under
mathematical control.
D-branes have found many interesting applications, but the most remarkable
of these concerns the study of black holes. One of the most dramatic recent
results in string theory is the derivation of the Bekenstein-Hawking entropy
formula for black holes obtained by counting the microscopic string states
which form a black hole. Bekenstein noted that black holes obey an "area
law", dM = K dA, where 'A' is the area of the event horizon and 'K'
is a constant of proportionality. Since the total mass 'M' of a black
hole is just its rest energy, Bekenstein realized that this is similar
to the thermodynamic law for entropy, dE = T dS. Hawking later performed
a semiclassical calculation to show that the temperature of a black hole
is given by T = 4 k [where k is a constant called the "surface gravity"].
Therefore the entropy of a black hole should be written as S =A/4. Physicists
have shown that this exact entropy formula can be derived microscopically
(including the factor of 1/4) by counting the degeneracy of quantum states
of configurations of strings and D-branes which correspond to black holes
in string theory. This is compelling evidence that D-branes can provide
a short distance weak coupling description of certain black holes! For
example, the class of black holes studied by Strominger and Vafa are described
by 5-branes, 1-branes and open strings traveling down the 1-brane all
wrapped on a 5-dimensional torus, which gives an effective one dimensional
object -- a black hole. More specifically, it can be shown that D-brane
techniques can be used to count the quantum microstates associated to
classical black hole configurations. The simplest case, which was studied
first, is static extremal charged black holes in five dimensions. It has
been showed that for large values of the charges the entropy (defined
by S = log N, where N is the number of quantum states that system can
be in) agrees with the Bekenstein-Hawking prediction (1/4 the area of
the event horizon).This result has been generalized to black holes in
4D as well as to ones that are near extremal (and radiate correctly) or
rotating.
S ~~[(XuXu
-2$u$u) - {£a£a
where X
=Boson field, ('u' and 'a' are dimensions of 10 and 16 respectively)
$
=Fermion field (2 component world sheet spinors) propagating along string
and transforming as a vector representation of the Lorentz group
The heterotic
string has the structure of an E8*E8 {or SO(32) } gauge symmetry and D=10
spacetime supersymmetry. (Simple bosonic strings were found to need 26D
but superstrings require 10D) The physical space is a tensor product
of the Right moving oscillator modes (fermionic) that include supersymmetric
degrees of freedom (10D). [these involve the right moving modes $u
and the right moving part of Xu] and
those left moving modes (bosonic 10D) that are responsible for Gauge symmetries
[these are the left moving part of Xu
and the £a.]
Red = 10 dimensional
field in which the Right moving oscillator modes are fermionic (both Xuand
$u have these) and the Left moving modes
(Xu field only) are bosonic. (The left moving
10D bosonic string combines with the right moving bosonic string to complete
a bosonic closed string).Because of the Right moving modes there
is consequently a supersymmetry between the bosonic
Xu and the fermionic $u ..as in typeII
string models. . viz
&Xu=ie$u_ ,,,,,,
,,, and &$u_=e&_Xu. where e is the
supersymmetry generator
Bold =16 dimensional fields which contain only
Left moving modes £a, therefore it only has gauge symmetry,
(probably an E8*E8 isospin symmetry of a compactified 16 Tori root lattice
space)
£a = originally 26D fermion coordinate field
that can be replaced by 16D bosonic coordinates that transform with isospin
gauge symmetry ie. containing internal quantum numbers. Together
with the 10 dimensional left moving bosonic field of Xu, these produce
the 26 free bosons necessary in the Veneziano string model.
The 10D supersymmetric space is itself compactified into
a Calabi-Yau manifold and 4D spacetime, which reduces the E8*E8 gauge
symmetry into the subgroups of U(1)*SU(2)*SU(3) that occurs in the standard
model (hopefully complete with graviton field and anomally cancellations).
The string action, is a field theory in 2 dimensions and
Xu(#1,#2) where u =1 up to D-1 dimensions
are coordinates for a string that is propagating in D space-time dimensions.
A more generalized 2 dimensional field theory that would correspond physically
to internal degrees of freedom that are free to propagate along the string,
such as the free fermionic field $a(#1,#2),
which could transform in the vector representation of the Lorentz group
SL(D-1, 1). It may seem counterintuitive that an anticommuting field should
transform as a vector -- a bosonic representation -- of SL(D-1, 1). This
choice means that $a(u=10) maps bosons to
bosons and fermions to fermions in the space-time sense (remember that
there is however a supersymmetry invoked by this introduction). However
since this is a 2 dimensional field theory, not a field theory in space-time,
and $a(u=10) transforms as a spinor under
transformations of the 2 dimensional world sheet, in perfect agreement
with the usual spin statistics. The Lorentz group SL(D-1, 1) is merely
an internal symmetry from the world sheet point of view and hence the
spin and statistics theorem says nothing about whether anticommuting fields
should transform as vectors or spinors under an internal symmetry. In
this manner we associate Lorentz quantum numbers to $.
In addition we can attribute other internal quantum numbers (as is necessary
in heterotic theory) by adding a 32D real Majorana 2 component spinor,
which transforms internally under a SO(32) gauge symmetry. This then insures
the canceling of any Virasoro-ghost anomaly since 2 Majorana spinors are
equivalent to one boson anomaly. Alternately and more interestingly, while
letting the $ fermionic field transform internally
as a Lorentz quantum number, we can account for the necessary 26D bosonic
requirement by introducing a 16D bosonic left moving mode £,
whose internal degres of freedom are subject to the E8*E8 symmetry caused
by compactification onto a 16 tori. The isotopic symmetry thus produced
can then account for the required spectrum of particles.
Hence the 2D world sheet string propagates in terms of
parameters #1 and #2 as it passes through a multidimensional space that
includes a 10D space-time, that has bosonic and fermionic field components
(i.e. it forms a supermanifold), which together eliminates tachyons. The
fermionic field is is made of 2 component world sheet spinors - each being
a Lorentz singlet (the world sheet parameters #1, #2 have a 2 spinor associated
with them, which can be mapped to a 10D fermion field that is space-time
covariant). There is also a 16D bosonic field, whose oscillator mode is
needed in order to eliminate ghosts (bosonic strings theories requiring
a total of 26D), and this can also be expressed as a 32 component spinor
field (2 Majorana spinors = 1 boson Virasoro-ghost anomaly) i.e. an SO(32)
gauge symmetry, or as is more favorable we could use the E8*E8 symmetry
of a compactified 16 Tori. The gauge symmetry therefore connects isospin
particle ie. fermions that carry internal quantum numbers. The left moving
modes are bosonic (producing gauge transformations) while the the right
moving modes are fermionic (producing supersymmetry)
The left/right asymmetry that is known to occur in the
weak interaction (and therefore the standard model), unfortunately leads
to anomalies in string theory i.e. there is an unwelcome breaking of the
symmetry when the string is quantized. Only two symmetries are known to
survive such necessary quantization viz. S)(32) and E8*E8. However at
present we usually can only apply perturbation theory and his allows too
many solutions. An exact method may isolate just one unique string theory
-- the one that accurately describes the vacuum, without yielding an embarrassingly
large value for the cosmological constant!
* * * * * * * * * * * *
More recent developments;
Braneworlds
The Higgs mechanism makes it look as though the
weak force symmetry is preserved at short distances (high energies) but
is broken at long distances (low energies).The weak Higgs field
has 2 components which are both zero when the weak symmetry is preserved,
however when one of these takes on a nonzero value it breaks the weak
force symmetry that interchanges the 2 Higgs fields. The symmetry is broken
spontaneously because all that breaks it is the vacuum -- the actual state
of the system, the non zero field in this case. However the physical laws
which are unchanged, still preserve the symmetry even though the physical
system does not. The symmetry transformations that act on the weak
gauge bosons, also act on the quark and lepton flavours and it turns out
that these transformations wont leave things the same unless they are
masslees. Now because the weak force symmetry is essential at high (GUT)
energies, not only is spontaneous symmetry breaking required for the gauge
bosons, it's necessary for these quarks and leptons to acquire mass as
well. The Higgs mechanism is the only way for all the massive fundamental
particles of the standard model to acquire their masses. At high energies
the internal symmetries associated with the weak force, still filters
out the problematic polarization of the weak gauge bosons that would cause
interactions at too high a rate.
However at low energies, where the mass is essential
to reproducing the measured short range interactions of the weak force,
the weak force symmetry is broken. In this mechanism, there are original
3 weak gauge bosons plus a Goldstone boson and after symmetry breaking
we have the massive W+- and Z bosons plus the photon, which is able to
travel in a massless mode through the Higgs vacuum unaffected, since it
has no weak (flavour) charge. The problem with GUT is that although the
Higgs particle has to be relatively light for weak symmetry breaking (~
250GeV as born out by experiment,) it is partnered another particle (X),
that interacts with it through the strong force and which has to be extremely
heavy [This in order to explain the stability of the proton, which would
otherwise decay due to the X particle allowing a quark to change into
a lepton]. In other words we are left with the problem that 2 particles
that are related by GUT symmetry have to have enormously different masses
(the weak and strong forces have to be interchangeable at high energies).
This hierarchy problem is made worse by the fact that QT requires
the value of the Higgs particle to be determined by contributions of virtual
particles which are of the order of the energy scale of GUT (according
to the anarchic principle in which any interactions that is not
forbidden by symmetry will occur). However these QT contributions (some
positive some negative), which must be added to the classical value of
the Higgs boson, are under GUT energy values 13 orders of magnitude greater
than the weak Higgs value! The situation is even worse when we consider
gravity since QT corrections now occur at the Planck scale (10^19Gev)
[Newton's law states that strength is inversely proportional to the square
of of the energy/mass and because gravity is so weak the Planck scale
is large Another way of phrasing the hierarchy problem is to ask why gravity
is so feeble]. Such a trickle down effect of QT contributions should therefore
make a large quantum mass determine the ultimate mass of other particles,
so that all end up rich in mass. Supersymmetry (SUSY) gives an answer
to this by allowing the positive QT contributions of the bosons to be
canceled by the negative contributions of the fermions. It achieves this
by first pairing all the fermions and bosons with superpartners, the Higgs
field then gets contributions from both particles and supersymmetric particles
and because the interactions with the two are different their contribution
to the Higgs particle's mass, cancel each other out.
Now in order to account for the lack of observed
superpartners, it is necessary to invoke a SUSY breaking, which
imbues mass to the superpartner, making it to large to to be stable or
created in particle accelerators. However once supersymmetry is broken,
flavour changing interactions are allowed which are not observed
in nature or at least are a lot more rare than predicted. These are processes
that change quarks or leptons into those of another generation (that is
ones that are heavier or lighter but with the same charge). Although an
electron and a slectron can interact via the weak force as can a muon
and smuon, an electron would never interact directly with a smuon. If
an electron were paired with a smuon or a muon with a slectron, this would
allow a muon to decay into an electron and a photon, something which is
never observed. However with SUSY breaking the now massive bosonic superparteners
no longer have the strong sense of identity of their partner fermions,
and this allows the (massive) bosonic superpartners to get all mixed up,
so that not only a smuon but also a slectron would be paired with a muon
for example. However this pairing of a slectron and a muon would yield
all sorts of interactions that are not observed. So although SUSY can
overcome the hierarchy problem it does lead to a flavour problem.The
question is how do we break the SUSY, but prevent the flavour problem
from occurring. One possibility for resolving the called flavour
problem is to resort to large dimensional branes (without SUSY),
which may also allow a remedy to the Hierarchy problem.
An alternative approach to SUSY in addressing these
and other problems, is Braneworld theory.Branes originated from string
theory (1989), in which D-branes (Dirichlet boundary conditions), were
used as ends for strings that move in the bulk space. At around the same
time p-branes were discovered as solutions to Einstein's field equation
in higher dimensions. These extended infinitely far in some spatial dimensions
but in the remaining dimensions they act as black holes. In some geometries
they are found to give rise to new types of particles that are not accounted
for in D-brane string theory. These p-branes are independent objects that
can wrap around a very small curled up region of space time, an act like
particles. In 1995 it was shown that D-branes and p-branes were actually
the same thing and that at energies where string theory makes the same
predictions as General Relativity, D-branes morph into p-branes. The way
in which this equivalence is best expressed is via the important notion
of duality(cf. *!*
above.) An important aspect of duality was revealed by Witten in 1995
when he demonstrated that a low energy version of 10D superstring theory
with strong coupling was equivalent 11D supergravity with weak coupling
(which could therefore be dealt with by perturbation techniques.Dualities
between all the contending string theories were established bringing about
a second revolution in string theory, namely M-Theory. In order to reconcile
the difference in dimensions it was realised that the strings were actually
membranes that extend in dimensions that were previously not recognized
due to their compact size and these have been identified as the p-branes.
[Eleven dimensional supergravity although not containing strings was already
know to contain 2D membrane solutions] The key was therefore the realisation
that rolled up dimensions are invisible at long distances or low energies,
making 11D supergravity with one dimension curled up equivalent to 10D
string theory [In 11D supergravity you need to know the momentum in 10D
whereas in 11D superstring theory you need to specify the momentum in
9D and also the value of the charge, i.e. 10 numbers have to be specified
in each case to make the particles correspond in the 2 theories. [Perhaps
this is an indication that these extra dimensions should be regarded as
auxilliary variables just as is charge} Ordinary uncharged strings do
not pair with objects in 11D and the partners of objects in 11D theory
turn out to be branes viz. charged pointlike branes called Do-branes.
The 2 theories are dual because for every Do-brane of a given charge in
10D superstring theory, there is a corresponding particle with a particular
11D momentum and vice versa] It was soon realised that it was possible
to formulate theories of higher dimensional branes within the context
of M-theory.
Mmathematicians also began to consider the possibility
of a higher dimensional universe in which the particles and forces reside
in a lower dmensional brane - - a Braneworld! The first example of this
was the HW braneworld (Horava-witten), in which 2 branes bounding the
11th dimension, were shown to be equivalent to the heterotic string, with
strong coupling (this is yet another example of duality). the new feature
of braneworlds is that it allows particles/forces to exist on seperate
branes and only able to communicate weakly via bulk particles such as
the graviton. Although strings representing particles and forces can be
trapped to branes there is no requirement to resort to them but braneworld
theory does assist SUSY in solving the hierarchy problem. [The difficulty
with this approach is that the SUSY needs to be broken if is to explain
why we observe particles but not the (massive) superparners.] This problem
results from the anarchic principle, and is due to the (virtual) quantum
contributions (especially at the GUT or Planck scale), to the Higgs particles
mass (which after all is responsible for imbuing mass to all other particles).
An alternative way out of this problem, is to assume
that sequestrating particles on a separate brane can prevent these unwanted
interactions that until now could only be restricted by symmetries. Basically
by sequestrating the unwanted particles on a seperate brane the anarchic
principle can be restricted. The graviton (or maybe the gauginos) are
able to travel through the bulk and are responsible for communicating
the SUSY breaking but since this breaking happens sufficiently far away
it will have very little effect. This graviton induced communication of
SUSY breaking is known as anomaly mediation. In this way the interactions
of the Standard Model remain the same as in a theory with unbroken symmetry.
So just as in a theory with exact SUSY unwanted flavour changing
do not occur. [A refinement of this concept is that other particles responsible
for flavour symmetry breaking are sequestrated on other branes, the breaking
being communicated to Standard Model particles only via particles in the
bulk Different flavours of quarks and leptons would be different because
they interact with a different brane at a different distance (the further
the distance, the smaller the mass induced), an effect termed shining]
These bulk particles although originating/travelling in higher dimensions
should still leave some sort of trace in our 4D world and are refered
to as Kaluza-Klein KK particles (a term which is also used in the T dualities
in M-theory, since in both cases, their energies a determned by the size
of the extra dimensions - - branes may be curled up in M-theory ). If
the extra dimensions are bigger the KK particles are lighter; if the world
is higher dimensional but with no branes then all familiar particles will
have KK partners. They would have exactly the same charge but carry momentum
in the extra dimensions.
The next stage in development was the realization
that extra dimensions rather than SUSY could explain the Standard model.
This ADD idea postulates that larger dimensions might explain the (apparent)
weakness of gravity and explain why the Planck scale and weak scale are
so different - - thus solving the hierarchy problem [The hierarchy problem
can be expressed in another way; why is the Planck scale so large when
the weak scale is so small or equivalently why is the strength of gravity
so weak] Essentiall the ADD model claims that the fundamental mass scale
that determines gravity's strength is not the Planck scale mass but one
much smaller (gravity's strength is inversely proportional to the Planck
scale) In these and subsequent developements , the larger the extra dimension,
the weaker the gravitational force in the effective lower dimensional
universe would be. The initial spreading out in the extra dimensions would
reduce the density of the force lines in lower dimensional space, so the
strength of gravity experienced would be weaker. If a Tev were the typical
energy of gravity, there would no longer be a hierarchy of masses in particle
physics. the Planck scale mass that we measure in 4D is large only because
gravity has been diluted in 'large' extra dimensions. If
these ideas are true then it means that it would be possible to create
black holes and KK particles at energies close to a Tev and also we may
be able to detect a deviation of Newton's inverse square law at small
distances.
Further developments involved warped passages
connecting these branes - - the RS1 theory of Randall and Sundrum [a warped
space is one in which the cross sectional dimensions have the same geometry
(e.g. flat), while the extra dimensions have a variable curvature]. This
comes about when we consider branes which themselves and the bulk space,
have energy and can therefore induce a curvature as we move away into
the extra dimension. By solving Einstein's field equation for a particular
braneworld we obtain a gravitational probability function in which the
strength deteriorates the further we move away from one of the branes
gravity is seen to be confined on one brane (the Gravitybrane which carries
positive energy ) and weakens as it heads towards the weakbrane (which
carries negative energy) upon which all the standard particles reside.
The warped space causes gravity to decrease at an exponential rate and
in this way we do not require a large separation between the 2 branes
and no contrived large number in order to explain the hierarchy. The huge
ratio of the Higgs masses is expected if gravity (Planck scale), is confined
near the gravitybrane, while the weak interaction is confined on the weakbrane
some 16 units away (giving a reduction by 10^16)
In order to accommodate the apparent unification
of the interactions that is indicated by the convergence of the strengths
at higher energies, work has revolved around the application of strings
which are allowed to move through the bulk These strings represent the
various standard model particles and their gauge bosons. Unlike the graviton
which must arise from a closed string, gauge bosons and fermions will
be either stuck on a brane or free to move in the bulk. With the warped
geometry model the extra dimensions are not so large and therefore these
interactions are not diluted so much No longer tethered to the weakbrane
they could travel anywhere in the bulk and have energies as high as the
Planck scale. Only on the weakbrane does the energy have to be less than
a Tev. Because these interactions would be in the bulk and therefore operate
at high energies, unification of forces would be a possibility. Also the
hierarchy problem in warped dimensions requires only that the Higgs particle
be on a weakbrane, so that its mass will be about the same as the weak
scale energy (the weak gauge bosons need not be stuck there but will automatically
have the correct masses). So the weak scale would be protected (at ~1Tev),
but unification could still occur at very high energies on the GUT scale,
without invoking SUSY (but warped extra dimensions instead) The implications
of this is that KK particles five dimensional black holes and strings
could be observed at energies accessible to the new particle accelerators
(tevatron and LHC)
A further development known as RS2 involves only
one brane in which the warped bulk space localizes gravity via
an exponential fall off. The standard model particles which are on or
close to the gravitybrane, only act weakly with the gravity field, which
although existing in 5D, behaves (due to the extreme warping of the bulk),
like 4D Newtonian gravity. In this highly warped space an infinite extra
dimension is possible and yet it would still appear as our 4D world. The
main points of this version is that a second weakbrane is found to be
unnecessary in determining the correct warping falloff of gravity. Hence
we just have a single brane determining the distribution of gravitons
which interacts with the Standard Model particles at some distance away
from this gravitybrane. So long as this function exponentially reduces
the Planck scale (producing the well known high value of the Planck energy
that is observed), then we overcome the hierarchy problem. The quantum
fluctuations effect for the Higgs particle is reduced, which in turn produces
realistic values for the particle masses and their gravitational effects.
By employing warped space, it becomes feasible to explain the existence
of higher dimensions, without the need to resort to the compactification
of the extra dimension (or at least it offers a supplementary method to
string theory). When gravity is localized in this way, physical laws behave
as if these extra dimensions weren't there, just as with rolled up dimensions.
Indeed by considering a negative energy on the gravitybrane (in addition
to the warped space due to the negative energy of the bulk space), the
brane itself is no longer flat and we can create a locally localized gravity,
in which the graviton function only produces a 4D interaction only in
a local region of our universe - - -the rest of space could look 5 dimensional
or more
Matrix theory applies a 2 dimensional matrix property
to each point in 10D stacetime and is used to explain the behavior of
Do-Branes which move through this space. Even though the theory does not
explicitly contain gravity Do-Branes act like gravitons Furthermore the
theory of Do-Branes mimics supergravity in 11 dimensions not 10. That
is the matrix model looks as if it contains supergravity with one more
dimensions than the original theory seems to describe. This has led string
theorists to believe that matrix theory is equivalent to M-theory. All
this tends to cause us to be cautious when talking about the reality of
these extra dimensions. As Ed Witten summarized " space and time
may be doomed" and N Seilberg says "I am almost certain that
space and time are an illusion" while David Gross states that "Very
likely, space and even time have constituents; space and time could turn
out to be emergent properties of a very different looking theory"
NEXT PAGE
|