

The following articles
are contained below;-
Millennium
Dawn
Philosophical
Considerations in Science
Dilemma's
In Physics and Religion
It's
About Time
Darwin's
Theory of Evolution
Idealism
and Realism in Physics
Infinity
And The Mind
"It was, of course, a lie what you read about my religious
convictions, a lie which is being systematically repeated. I do not believe
in a personal God and I have never denied this but have expressed it clearly.
If something is in me which can be called religious then it is the unbounded
admiration for the structure of the world so far as our science can reveal
it."
"A knowledge of the existence of something we cannot
penetrate, our perceptions of the profoundest reason and the most radiant
beauty, which only in their most primitive forms are accessible to our
minds - it is this knowledge and this emotion that constitute true religiosity;
in this sense, and this alone, I am a deeply religious man."
"I believe in Spinoza's God who reveals himself in
the orderly harmony of what exists, not in a God who concerns himself
with the fates and actions of human beings."
: "My religion consists of a humble admiration of the
illimitable superior spirit who reveals himself in the slight details
we are able to perceive with our frail and feeble mind."
A. Einstrein..
"WHAT WE CAN KNOW OF THE WORLD CONFORMS TO CERTAIN SYNTHETIC A PRIORI
CATEGORIES, WHICH ALTHOUGH WE RECOGNIZE BY EXPERIENCE DO NOT ARISE
FROM EXPERIENCE. THESE CATEGORIES (E.G. SPACE AND TIME) ARE LAID
DOWN BY THE MIND AND TURN SENSE DATA INTO OBJECTS OF KNOWLEDGE"
P. Bennett. .
Millennium
Dawn
At the beginning of the last century, there were just two seemingly
small clouds, which obscured our otherwise impressive view of the physical
world. Most of physics was believed to have been well understood, there
just the small problem of the inability to detect the luminiferous ether
and the statistical anomaly in black body radiation. These ‘small’
clouds on the horizon did however grow to gigantic proportion, casting
a gloomy shadow over the physics community which resulted in two great
revolutions viz. Relativity and Quantum
theory.
The inability to detect the ether was an indication that our understanding
of space and time was flawed and eventually culminated in Einstein's general
theory of relativity, which not only discarded the notion of an absolute
space and universal time but also demonstrated that gravity was a manifestation
of a curvature in the space-time continuum. Matter tells space and time
how to warp and these in turn determine how test particles move (along
geodesics of maximised space-time intervals, or proper time). Henceforth
the laws of physics were no longer valid under Galilean transformations
but instead had to be Lorentz covariant and Maxwell’s equations of
electromagnetism, were unintentionally the first to be written in this
form.
The ultraviolet catastrophe that had occurred in the theoretical
study of black body radiation was yet another example of where ‘a
conflict was brought to light’. Using the two pillars of classical
physics (Maxwell’s electromagnetism and Newtonian mechanics), it
was possible to predict the distribution of frequencies emitted by a perfect
black body radiator. However the embarrassingly infinite amount of radiation
that is predicted at the shorter end of the spectrum, could only be avoided
if we introduce a quantised (instead of continuous), emission by the atoms
that were in thermal equilibrium with their radiation. The energy is therefore
released in discrete amounts that were proportional (via Planck’s
constant) to the frequency. Planck himself was troubled by the implications
of his own radical alteration but far worse was yet to come. Einstein’s
paper on the photoelectric effect showed that it was not that thermal
oscillations emitted discrete amounts of electromagnetic waves but that
light (and other radiation) has an inherently particulate nature. This
view was emphatically reinforced by Compton’s electron scattering
experiment, which demonstrated that X-ray quanta possessed the same kind
of momentum that is associated with particles in collisions.
A further challenge to classical physics came from the fact that
Rutherford’s alpha scattering experiment showed that atoms consist
of a positive nucleus orbited by electrons. This in turn conflicted with
electromagnetic theories since such accelerating charges should continuously
emit radiation and spiral into the nucleus. At the same time De Broglie
had suggested, that entities such as electrons, could be regarded as possessing
wavelike characteristics. Indeed J.J. Thomson was awarded the Nobel Prize
for demonstrating that electrons are particles while his son later received
the same honour for showing that they were waves!
Also experimental data regarding the change in the specific heat
of materials as they are cooled to very low temperatures, can only be
explained by using the phonon model of lattice vibrations. Indeed it was
the partial success of Einstein’s earlier attempt at such a quantum
description of specific heat, that was particularly influential in causing
the widespread acceptance of quantum theory. However it did take the first
quarter of a century before the downfall of classical physics was finally
complete and the early efforts of Einstein, Planck and De Broglie were
shown to be a manifestation of the far more sinister reality of Schroedinger’s
wavefunction and Heisenberg’s uncertainty principle.
At the dawn of a new century (indeed a new Millennium) the main
cloud that we face in physics, is the inability to reconcile General Relativity
(and hence gravity) with Quantum Theory. It may not be fully appreciated
for quite some time, as to how big a revolution in our understanding this
will require, although there are indications that it will be considerable.
On a wider front, the other great challenges will include an understanding
of the human mind (particularly consciousness) and what constitutes life,
as opposed to other complex chemical systems.
The last century did leave us with the legacy of the nuclear age,
one that initially promised a Utopia but did so much to disappoint. The
new century could unleash a far greater jeopardy, since the bio-technological
time bomb that we are in danger of releasing, may be far more perilous
than the nuclear bomb that we have learnt to live with so far. There is
consequently an even greater need for the general public to become more
educated in science, but without becoming professionally indoctrinated
Philosophical
Considerations in Science
According to Raven, the dilemma in which honest students found
themselves, arose out of the need to maintain their ‘religious experience
or moral responsibility’ whilst retaining their scientific integrity.
In his analysis ‘an agnostic humanism or an authoritarian supernaturalism
seemed an obvious answer to their dilemma. ie. either a release from ecclesiastical
dogma, faith in progress and a belief in man being the measure of all
things or the unconditioned acceptance of theology in dictating a moral
code and the spiritual reality beyond science.
James Maxwell provides a good example of how such an ‘honest
student’ came to terms with the task of advancing the frontiers of
scientific while maintaining the spiritual truths of his religion. Maxwell
was imbued with a deep mystic piety, characteristic of his native Gallaway
and adopted a theological basis to nature that involved a deep romantic
appreciation. This is particularly exemplified in his formation of his
statistical laws of thermodynamics, in which he realised that the only
satisfactory way of explaining the observed facts was to implement an
epistemology of acausal chance but at the same time he retained a belief
in ontological determinism.
Such a nuance resulted directly from his personal need to reconcile
science with religion. At that time there was abhorrence towards deterministic
materialism and its proclivity for atheism, but there was also a reaction
against Darwin’s theory, which deemed that chance rather than design
was the cause of evolution. To have accepted the materialistic ontology
of Lucretius, with its violation of atoms and deification of chance would
have sacrilege the omnipotence of God. Whilst replacing the ontological
randomness of Lucretius with the apparent randomness of Laplace, he regarded
the macroscopic world as one of ‘chance and change’ in which
his epistemology is akin to the certainties of the census taker rather
than to Laplacian probabilities which was steeped in determinism. Such
a stance was not only pleasingly detrimental to the epistemology of determinism
but also succeeded in maintaining an ontology that was amicable to a teleological
view of God
In order to emphasis the
distinction between the apparent randomness due to our inability to know
and ontological certainty, Maxwell invented a being (unfortunately dubbed
‘Demon’ by Kelvin), who could violate the Second law of thermodynamics
due to his omnipotence, thus showing the law to be of statistical rather
than of absolute nature. We now know that the entropy associated with
information makes any such proposal a theoretical impossibility but this
does not diminish Maxwell’s GEDANKEN, since to him the Demon was
analogous to God and hence not subject to materialistic constraints –
being a creature of divinity, he was not limited to energy requirements.
Likewise, being faced with the concept of a universe which was dissipating
under the Second Law, he again related to a divine being to whom the universe
is always ordered and controllable and from which he can always extract
work.
The debate over free will versus determinism had been a source
of contention between the Calvinists (whose hellfire attitude denied the
former) and the Armenians whose moral teachings were based upon volition
– the child being the father of the man, rather than the wretched
being eternally damned. Maxwell, having allegiance towards the latter,
was consequently averse to the use of determinism as applied to man. Being
aware of the transitory nature of scientific theories, he did not want
to attach them to religious ideas (whose knowledge to him was absolute)
since it ‘may help to keep the hypothesis above ground long after
it ought to be buried and forgotten.’
Whilst desiring consonance between science and his personal belief,
he was not prepared to make religious appeasement’s which he knew
would become an embarrassment when that particular theory became obsolete.
He realised the approximate nature of different scientific theories and
was likewise tolerant to the various religious denominations, felling
equally at home in Baptist, Presbyterian or Anglican churches. In this
way he avoided having to interpret religious scriptures in terms of the
prevailing scientific view. He believed that behind the empirical realities
of nature and the various sectarian postures of religion, lies a deeper
level of reality and did not wish any of his conceptions to be ‘carried
beyond the truth by a favourite hypothesis.’
His most monumental work, that of the unification of electrostatatics,
magnetism and light had also been driven by his conviction for a creative
element of the universe – a conviction which inspired, guided and
justified his scientific endeavors. He attached great significance to
both inner experience as well as insights from the external world –
what he described as the ‘Two Gateways to knowledge. His radical
evangelical beliefs had both directed him in life and supported him in
death.
Being born a Jew it was taken for granted that Emile Durkheim would become
a Rabbi like his father. However during his student day he became more
secular but with a strong bent towards moral reform and he tended to take
a silent agnostic view upon whether religious beliefs did have a divine
basis outside its social function. His personal ideology was somewhat
stoical, believing that "efforts and even sorrow are more constructive
to the spiritual progress of the individual rather than pleasure or joy."
Durkheim's approach relied heavily on scientism (particularly biologism)
by which categories of science are extrapolated into other fields of knowledge,
such as ethics and theology. Although believing in the autonomy of social
facts, without needing to resort to reductionalist explanations, his functionalism
did rely upon biological analogies. Durkheim was a socialist for
whom Homo Faber had the power to drastically influence his own environment.
Natural selection did not therefore play such a powerful role upon society
as it had done with the development of life itself -- modes of expression
depending upon cultural rather than genetic inheritance. In his view morality
is only justified in its social acceptance by the majority, taboos and
rituals included and in some respect his tolerant treatment of all religions
is somewhat disconcerting as he states " The most barbarous
and most fanatic rites and strangest myths translate some human need of
social life...."
For Durkheim there is no conflict between religion (ads he views it) and
science with which he attempts to explain it -- the very act of which
presupposes it. Religion fills the void left by science, with speculation
and the resulting conflict between scientific reason and religious faith
often results in the outpouring of idiosyncrasies. He states "Science
is fragmented and incomplete, it advances but slowly and is never finished
but life cannot wait". The theories which are destined to make men
live are therefore obliged to pass science and complete it prematurely."
He therefore regards both the religion and science as attempting
to satisfy the need to connect things with each other in order to obtain
a greater understanding and even views scientific logic as being of religious
origin, although the former purges superfluous elements and incorporates
a spirit off criticism. Scientific thought is therefore regarded as a
more refined form of religious thought, from which it has developed both
of which are ultimately founded upon faith. Whereas religion claims the
right to go beyond science, Durkheim personally eschews such metaphysical
beliefs but instead regards religion as playing a crucial and unavoidable
social role.

The Danish physicist Neils Bohr, pioneer of modern atomic theory,
was an incarnation of altruism. During the war, he had assisted refugees
escape Nazi tyranny and had even donated his Nobel Prize to the Finnish
war relief, while after he was instrumental in establishing the ‘Atoms
for peace’ conferences. His mother was of Jewish descent but his
upbringing was that of a traditional Protestant. During his youth he was
an avid reader of his compatriot Soren Kirkegaard, a religious thinker,
regarded as the originator of Existentialism (Leap of Faith=Quantum jumps).
Kierkergaard, had reacted against the wave of intellectualism that had
threatened to engulf Christian belief at that time and in addressing the
paradox of Jesus necessarily being the embodiment of both men and God,
he wrote ‘When subjectively (inwards) is the truth, the objectively
defined becomes a paradox and the fact that the truth is objectively a
paradox shows in turn that subjectivity is the truth’
It is quite possible that Bohr reflected upon this view when he
came to grips with the Quantum postulates, in
which the question of whether an electron (or a photon) is a particle
or a wave is meaningless and leads to a paradox when viewed objectively,
being only answerable in terms of the subjection description of a quanta.
[Kierkigaard had similarly shifted the focus of attention away from the
contemplation of who God is to how God relates to us –in other words
how we interact with him].
Independently of Heisenburg’s Uncertainty principle, Bohr
had formulated his ‘framework of Complementarity’(1927), a new
feature of natural philosophy which means a radical revision of our attitude
as regards physical reality’. Bohr maintained that any distinction
between observing systems and the observed object are arbitrary made by
the description of that interaction. The anti-realism implication of recent
developments (viz matrix mechanics) had become a continual torment to
Bohr. ‘How can our lord possibly keep this world in order?’
Bohr could have kept our classical framework and merely discarded the
relativistic interpretation but in fact he did just the opposite, what
he rejected was not realism but the classical version of it, which he
replaced with his complementarity – not a theory or a principle but
an epistemological framework!
Bohr thus obtained spiritual solace from his new found realism,
in which certain dynamic attributes (eg position and momentum) are contextual,
while the static attributes of mass, charge and intrinsic spin are innate.
However the philosophical framework which he tried which he tried to instigate
was intended to extend beyond the domain of quantum theory but unfortunately
it often became incarcerated by if not mistaken for the Critical positivism
of the Copenhagen interpretation, which simply endorsed which simply endorsed
the unavoidable use of conjugate pairs of variables, for which precise
information was simultaneously denied. Bohr believed that his ‘epistemological
lesson of complementarity’ had potential in solving many age old
dilemmas such as mechanism versus vitalism in biology, free will vs. determinism
in psychology, or nature vs nurture in anthropology; he dreamt of a ‘conceptual
framework’ which could be the ‘unity of knowledge.’
It was during the ensuing debate with Einstein that the full implications
of what Bohr admonished became apparent- a favourite quotation of his
being Schiller’s Sayings of Confucius ‘Only wholeness leads
to clarity/and truth lies in the abyss.’ Einstein’s argument
involving the EPR experiment appeared to demonstrate that an electron
did indeed posses more information than was extracted by an observation
(thus demonstrating that quantum theory failed the completeness criterion.)
However Bohr’s counter was his belief that the whole was greater
than the sum of the parts. Although some earlier influences towards such
beliefs can be traced back to discussions with his father Christian, brother
Harold and the philosopher/friend Neils had been considerably influenced
by eastern religious beliefs. Having spent some time touring the orient
(in particular China) when knighted, he chose the Taoist symbol of Yin
and Yang as his coat of arms1 this pristine symbol of harmony represents
a holism that is very similar to that enshrined in Bhor’s complementaity
framework.
Up until then western philosophy had tended to find reality in
substance, whilst oriental philosophy had found it in relation. Bohr wrote
‘isolated systems are abstractions, their properties being definable
and observable only through their interaction with other systems.’
Just as Yin complements Yang, so does position complement momentum as
does energy with time. Although Bohr was reticent upon ontological maters,
he in effect had made science more spiritual and was quite likely struck
by the similarities between empirical scientific endeavour and primordial
eastern belief, in which space, time and causality are like a glass through
which the absolute is seen; in that absolute there being neither space,
time or causality [Heisenburg had likewise become deeply impressed and
guided by allegorical eastern beliefs, during his stay in India.] This
dynamic interplay of Yin and Yang as exemplified in the Uncertainty principle
or the complementarity of a wave-packet is even more apparent in the latter
more successful theory of Quantum electrodynamics by which even a vacuum
is a fluctuating continuum of ephemeral particles.
Bohr was one of the first to realise that physics and Eastern beliefs
were coterminous in their attempt to understand reality beyond our immediate
senses. He tried to point a way in which the idea of complementarity could
throw light upon many aspects of human life and thought, even venturing
comments upon its relevance to art, music and religion and the age old
problem arising from the fact that ‘man both acts and is the spectator
of his actions in the drama of existence.’ His life long consolidations
of complementarity (during which he wrote more than 20 varied papers)
had probably therefore been inspired at first by the religious teachings
of Kierkergaard and later by oriental beliefs which emphasis harmony,
wholeness and rhythmical interplay. This would have endorsed a conviction
for the personal subjectivity of God and the moral belief that man cannot
insulate himself from his deeds or his environment, his actions having
repercussions that may ultimately affect his own wellbeing. For Bohr,
this perhaps would have been a fitting atonement for the loss of causality.
********************************
During the Weimar republic after the first world war, Spengler's book
" Decline Of The West" became very influential amongst intellectuals.
The outlook of the Weimar milieu, was ne-oromantic and existentialist;
it tended to build a future out of its past, returning to the romanticism
of Schiller and Goethe. Spengler Idealism was hostile towards the ideology
of the exact sciences and his philosophy influenced many including Weyl,
Brouwer, Heisenberg and Schrodinger. As a result, intuition rather than
logic became favorable in mathematics, while destiny rather than causality
tended to dominate in science. The two main defenders of the traditional
view were Hilbert, who defended the primacy of logic in the foundation
of mathematics and Einstein who defended the primacy of causality in
physics. However, the Spenglerian ideology of revolution triumphed both
in physics and mathematics, since Heisenberg discovered the limits of
causality in atomic phenomena and Godel the limits of formal deduction
and proof in mathematics! However eventually the vision of Spengler
became irrelevant, since Chemists who had never heard of him could use
QT to calculate covalent binding energies, while the discoveries of
Godel did not lead to a victory of intuitionism but rather a recognition
that no single scheme of mathematical foundations has a unique claim
to legitimacy
Dilemma’s
in Physics and Religion
Dilemma is an old Greek word, which means that one is faced with
two possible choices, non-of which is acceptable! Consider the riddle
of the prisoner who is sentenced to death. The judge decrees that the
last statement of the condemned man shall decide the method of execution.
If his last statement to the executioner is true he will be beheaded if
it is false he will be hanged – the choice is therefore in the hands
of the prisoner. On the morning of his execution he whispers his final
words to the executioner, who being faced with a dilemma, decides to release
him. What were the prisoner’s words? [The answer is below]
A well known dilemma in Physics is ‘what happens when an irresistible
force meets an immovable mass.’ The solution is actually quite straightforward
once one realises that the phrases need to be clarified. Referring to
Newton’s Second law F=MA, there is no such thing as an ‘immovable
mass’ (object), since even the smallest of forces can move the largest
of masses, although the acceleration would be minute. Also the concept
of an ‘irresistible force’ needs to be clarified, since as before,
even the smallest of forces produces movement (acceleration) on the largest
of masses, if there is no opposing force to balance it. Hence if a force
is to be considered irresistible it must be confirmed that it is not possible
anywhere in the Universe to provide another force of equal magnitude to
oppose it.
There is a similar dilemma in religion, which questions the existence
of God, since he is supposed to be both omnipotent and benevolent. However
Evil exist either in spite of his efforts (which precludes him being omnipotent)
or because of him (hence he is not benign.) The inability to resolve the
dilemma in its present context indicates that the very concept of God
needs to be clarified. Therefore, if one asks if God exists, the possible
answers could be ‘Yes’(Deism), ‘No’(Atheism), ‘its
not possible to decide’(Agnosticism) or that the question (as it
stands) has no meaning. There are examples in physics in which questions
have no meaning, such as “is an electron a particle or a wave.”
[The Prisoner says to the executioner ”You will
hang me”].
It’s
About Time
St. Augustine once stated that God did not create the universe
at a given moment in time but rather that time was created with the universe.
This showed considerable foresight, in that it is only this century that
physicists have firm evidence of the big bang, in which space and time
were created along with all the matter/energy of the universe. However,
there have been those who posit that only matter and motion exist and
recently, even some physicists have doubts about whether time actually
exists. Immanuel Kant believed that what we can know of the world, is
subject to certain synthetic a priori categories, that are laid down by the mind, which
although we recognize by experience,
do not arise from experience.
Space and time were cited as such examples, which act rather like filtering
lenses by which the brain turns sense data into objects of knowledge.
The physicist P. C. W. Davies remarked that we may not fully understand
time until we understand the human mind and even Einstein
originally believed that space and time are modes by which we think rather
than conditions in which we live! [He once mischievously said that if
you place your hand on a hot metal plate, time moves slowly but when you
are sitting next to a pretty girl, it goes quickly – that’s
relativity]. His later theory of General Relativity (GR) did however give
a more ontological reality to space-time, which supplanted the primacy
of gravitational mass. Quantum theory (QT) was
however difficult to reconcile with the space-time of special relativity
and this was only achieved by the introduction of spinor mathematics and
necessitated a field theory. The space-time of GR is still incompatible
with QT, since spinor manifolds do not avail themselves to Riemannian
technique and more importantly, the unitary groups that dictate interactions
in QT are not compatible with the unimodular group of relativity (unless
one resorts to supermanifolds).
As physical theories
have progressed our notion of time has been continually revised. The Galilean/
Newtonian view, is that time is absolute and that everyone can agree upon
what events are simultaneous, no matter where they occur. This is what
is now regarded mathematically, as an example of a fibre bundle i.e. a bundle whose base space is time and whose fibres are
that of Euclidean 3-space. Minkowski demonstrated that space and time
are inextricably linked, forming a 4-dimensional manifold as illustrated
by Einstein’s 1905 paper on Special Relativity. By 1916, an extension
to a general (non-inertial) co-ordinate system showed that time is slowed
down (and space is warped) by gravitational mass. More recently Penrose
has developed theories using projective twister space (rather than space-time)
which he believes is a fundamentally better manifold for structuring physical
laws. Hawking
on the other hand believes that QT is the way forward, although he does
utilize an imaginary time co-ordinate.
There have been several speculations as to the possibility of time travel,
most of which rely on the notion of warped space time. Special Relativity
is itself completely consistent with time travel into the future (moving
clocks run slower**) but traveling into the
past could lead to paradoxes. If a man can travel into the past he could
change events (e.g. kill his grandfather) which would prevent him from
ever being born in the first place. In 1949 Kurt Godel found a solution
to Einstein's field equations, in which a static universe would be stable
providing it rotated sufficiently fast (the centripetal acceleration is
in balance with the gravitational attraction of the whole mass in the
universe). He found that such a universe would result in a curving around
of space-time in such a way that traveling in closed loops, would not
only change your displacement but would also allow you to travel backwards
in time. Since a rotating inverse is not the case, the next best option
is inside a spherical black hole (which are believed to be quite common),
where the space and time coordinates also become interchanged. However
there is no way of escaping from a spherical black whole once you have
passed the event horizon. There may however be a way to circumvent this
problem, if one could create a rotating cylindrical shaped black
hole, whose rotation would allow you to escape from being dragged down
into the singularity, but such structures may not be stable. Also there
are worm holes that allow distant regions of space to be locally connected
by a short cut through space and which also suggest the feasibility of
backwards time travel, however these structures are also believed to be
fundamentally unstable for any would be time traveler.
Yet another possibility arises from the study of cosmic strings; when
two such entities come together it can be shown from topological considerations
that it may be possible to travel backwards in time by moving in a circular
path around the 2 strings. However such cosmic strings have not yet been
identified in the universe. Also any such time travel machine would only
allow you to travel back to the time in which the devise was first built
- this is often cited as the reason why we have not been visited by a
more advanced civilization from our future. As already mention backward
time travel can lead to dilemmas. For example imagine that one day a girl
physicist discovers a new solution written by Einstein, which describes
the workings of a feasible time machine. Having the technology to produce
such a machine, she travels back in time to visit Einstein and shows him
the solution which he then records (and is subsequently discovered by
the girl). The paradox then arises as to who actually discovered the solution!
Finally an interesting scenario has been put forward concerning the rapid
expansion in computer technology.
Future
civilizations will have sufficient computer power (especially with the
advent of quantum computers) to create perfect virtual reality universes,
which they will be able to run backwards and forwards in time. [It has
been recently demonstrated that even installing simple rules on a computer
program, can cause the evolution of quite organised systems, which are
then able to evolve and survive on their own.] Indeed they would quite
easily be able to run millions of such universe in parallel, each of which
permits time travel for those in control. We then arrive at the disturbing
realization that, statistically speaking, ours is more likely to be one
of these virtual universe set in the past, rather than being the
actual real universe which exists only for this one future
civilization (also we are clearly not sufficiently advanced to be that
universe).
The fact that time appears to flow in a forward
direction is also a peculiar property and is enshrined in the 2nd
law of thermodynamics. This statistical based law is not however the only
physical phenomena that indicates an ‘arrow of time’. Certain
sub atomic events involving the weak interaction are known to be time
asymmetric (specifically charge parity CP violation) as is the collapse
of the quantum wavefunction itself and indeed decoherence theory. [The collapse of the wavefunction may
be an effect of, an as yet unknown theory of quantum gravity, which itself
is probably time asymmetric as well as non local.] Also in cosmology the
universe expands rather than contracts with the forward flow of time.Other
notions
have built upon the block universe approach to time that exists in relativity.
As with space, time is regarded as an axis that can be traversed in both
directions and some have proposed ideas that are based upon action potentials
moving backwards in time from the future, to influence the present.
One of the most popular approaches in fundamental physics, is that
of string theory, in which the Lagrangian, is that associated with the surface being swept out by a string,
rather than that of a point like particle
which, as it moves through time sweeps out a curve. However instead of the 4 dimensions of space-time we have (according
to the most recent version), 11 dimensions, which became compactified
during the spontaneous symmetry breaking that occurred in the early universe.
Hence not only sub atomic particles but time itself (and also space),
is comprised of the dynamics/topology of these strings.
An increasing number of physicists have therefore started to take
the view, that it is our (inadequate) concept of time that may be responsible
for some of the intractable problems that face QT and GR.[Particularly
relating to the asymmetric collapse of the wavefunction but also a QT
of gravity implies quantised space-time!]. Indeed J. Barbour believes
that time does not exist but is merely an illusion. He has a tentative
theory, which involves stationary cosmological wave functions (akin to
that used in the Wheeler-DeWitt equation) acting upon a configuration
space of the whole universe (referred to as Platonia). Of course in this
cosmic wavefunction, we must also include the human mind but I am still
not convinced that this will be sufficient to completely justify Barbour’s
claim of ‘The End of
Time’ in physics. As Hume would say, how can something that exists
as a series of states (the Nows), be aware of itself as a series? (cf.
Relativity section under Quantum Loop Gravity, which also eliminates the
use of 'a background time along which everything flows')
The concept of both time and God are very useful/important to civilisation,
however it is possible that something as seemingly self-evident as time,
may not actually exist after all.
** This time dilation
effect has been accurately verified on many occasion. Specifically for
man it has been estimated that the worlds most experienced cosmonaut has
reduced his aging by one fiftieth of a second as a result of all his time
spent orbiting the Earth. This calculation was based on the speed at which
he has been traveling (producing a minute slowing down in the passage
of time) and also the reduced gravitational field compare to that at the
actual surface of the Earth (this causes an even smaller speeding up
of the flow of time).
Darwin's Theory of
Evolution
Both Wallace and Mivart provide examples
for Young's axiological perspective of Victorian naturalism, in which
science
and religion shared many of the same values. In particular they wished
to obviate any materialistic interpretations which Darwin'stheory might
attach to evolution (a term which Darwin himself never used in his "Origin
of Species")Wallace being cofounder of the theory, supported the
mechanism of natural selection, although due to his egalitarian beliefs,
he did not wish the theory to dictate a Laissez-faire attitude but instead
advocated a benevolent welfare society, which was not subject to materialism.
He believed that although the theory explained the physical evolution
of species, it did not fully account for
the emergence of mankind. To him, Darwinism was not incongruous with a
spiritual dimension of human existence - on the
contrary its shortcomings in this area lends support to human existence
- on the contrary its shortcomings in this area lends support to a belief
in the spiritual development of man which is independent of natural selection.
Mivart on the other hand proposed that Darwin's theory contained many
anomalies and that it only described a subordinate action of a more 'divine
natural law which had been laid down in the beginning by the creator'.
Being a Catholic, he was more sensitive to to the claims of Darwinism,
which conflicted with his metaphysical beliefs regarding design and creation.
Such deference regarding the church was not however shared by Wallace,
who did not specifically seek to reconcile evolution with theology. Although
not a Christian,Wallace's dualism did extend to a belief in the spiritual
world which transcended the epistemology of Darwin, who himself was reluctant
to engage in any metaphysical speculation as to the origin of the soul
or that of life itself. Wallace did not therefore dispute the material
evidence that different species had evolved from a common origin along
separate paths in which natural selection was a deciding factor but he
did make human beings an exception to the theory, whose spiritual development
he attributed to the intervention of an 'Unseen Universe.'
Survival of the fittest was a viable theory in explaining the large
diversity of species and a great deal of evidence of its
occurrence had been collected but Wallace also realised its inadequacy
and proposed that the very notion of natural selection can be used reprehensibly
when applied to mankind's 'intellectual and moral nature', since the development
of these in man's ascent, cannot be correlated to any such external pressures
and thus requires another prime motive. His conviction that the spiritual
nature of man evolved along disparate route to natural selection was,
an attempt to compromise science with belief. Wallace's spiritualism offered
an alternative to the excretory 'heat death' scenario and attached importance
to moral values; our happiness and spiritual progress depending on the
way we conduct ourselves in the material world, which exists for this
sole purpose --death being merely a transition from this material existence
to the spiritual life. His view is contrary to the theological dogma that
man being the created in communion with God had fallen into sin by Adam's
disobedient act. Instead he regards original sin as being the animal nature,
inherent in brutes, away from which our spiritual perfection is evolving,
by means which are independent of natural selection. Wallace argues that
the successive development of primitive savages is completely independent
of their cultural growth, since in Darwin's theory it is variations that
are immediately useful for survival, which become maintained and not characteristics
that will be of some use later (Mivart applies a similar reasoning when
criticizing physical discrepancies) and in this context there seems to
be stimulus for the growth in mathematical, musical or artistic faculties
in primitive savages, let alone animals. He stresses that 'no creature
can improve beyond its necessities for the time being' and although beneficial
mutations may arise, the occurrence of genius occupies such a small percentage
of the population, Wallace believes it unlikely to have much of an impact
upon the evolution of mental aptitude, since intellectual development
had not been prone to to natural selection and such mutations would consequently
become swamped by populous. "We have to ask therefore, what relation
the successive stages of the mathematical faculty had to the life or death
of its possessors."
Mivart however being a deist, concentrated his attack upon the inability
of Darwinism to explain all the biological variations that occur in nature.
He is thus trying to illustrate that another (divine) force, other than
natural selection is necessary to account for such phenomena as adaptive
radiation and convergence of species. Citing the absence of certain transitional
fossils he criticises the continuous variations of Darwinism and instead
advocates a punctuated evolution (salutation) which is not subject to
environmental pressures. In his 'Genesis of Species' he states "Another
difficulty seems to be the first formation of the limbs of higher animals.........how
are the preservation and development of the first rudiments of the limbs
to be accounted for ---such rudiments being, on the hypothesis in question,
infinitesimal and functionless?"
Mivart specifically mentions discrepancies with regard to the development
of baleen in the mouth of the whale and the
peculiar provision of the young kangaroo in relation to its sucking habits,
maintaining that the utility of certain factors which differentiated related
species, was either non existent or became existent only when the difference
had become fully developed. In the case of the baleen system although
obviously useful to the whale, any intermediate stage in its evolution
could not have been beneficial (he does not concede that any such embryonic
organs may have had a different use from the completed version.) Mivart
is evidently attempting to diminish the status of Darwin's theory by illustrating
that it is insufficient to explain the prime cause for the diversity of
life forms and indeed Darwin's pre-genetic theory did lack any viable
explanation as to the mechanism of heredity and mutation. In respect of
chance variation and natural selection -- which he regarded as having
only a secondary control -- he proposes that 'an internal power or tendency
is an important if not the main agent in evoking the manifestation of
new species on the scene of realised existence' although his reasoning
is somewhat tautological. He also uses fossils/geological evidence upon
which Darwinism is based in order to highlight its technical shortcomings
(at that time plate tectonics and continental drift were not established)
and there were considerable evidence to illustrate that certain transitions
amongst species were not smooth but more catastrophic or punctuated. Ironically
Mivart's attempted mediation, resulted in him being 'excommunicated' from
both his catholic and scientific brethren.
Wallace also uses the idea of a sudden insurgence amongst life forms
but confines his dissertation to that of the mental spheres. He mentions
several examples from the anthropology of civilisation in which certain
cultural upheavals took place which were in no way related to the need
for survival of the Lamarckian influence of the environment. He writes
"the barbarous conquerors of the east, Timurlane and Gengkis Khan
did not owe their success to any superiority of intellect" but despite
this there
are associated cultural revolutions which have occurred throughout the
ages independent of natural selection.The musical
development made by the Hindu and Egyptians, Greeks sculpture and geometry,
the renaissance, Enlightenment and many more cultural plateaux are regarded
by him as an example of unexplained bursts of human intellect, suddenly
appearing upon society without any prerequisite.[He does not consider
them to be merely bi-products of intelligence factors, which are subject
to selection]
However it is not only in civilised western man that Wallace produces
examples, he also believes that there is evidence of an unseen agent in
pristine tribes. He is quite prepared to accept that man had descended
from primitive animals but that natural selection only caused the impetuous
for physiological change. Wallace refutes the existence of certain mental
qualities (humour,moral conscience, sense of beauty,religious revelation
etc.) in animals or that they can be developed to that extent in humans
by means of natural selection, since no such stimulus exists for their
production. He does not give credence to the belief that cunning and ingenuity,
required for adaptation can inherently give rise to such qualities. Ethics
and altruism in his view are not agents of survival and he does not consider
that co-operation amongst individuals leads to a more viable fitness as
a group. Instead special reverence is given to abstract faculties which
he considers far removed from the genetic imperative associated with the
struggle for existence. These faculties he claims are almost non existent
in savages but appear spontaneously in civilised races. Another mode of
attack that Wallace uses is to illustrate that just because a theory provides
a reason for certain events to have taken place and is accurately descriptive
of the way things are, does not necessarily mean that it is complete in
itself. As an example he aptly states Lyell's original belief that the
Earth had been sculptured solely by the upheavals and depressions of land
and the denudation of wind and rain, until the study of glaciers showed
that other agents were responsible for certain relief
features of the Earth. Both Wallace and Mivart do however share common
ground upon their views of morality-- to which they attach a transcendental
significance -- as neither believe that natural selection could be responsible
for its emergence in man. Wallace tells us that "the love of truth,
the delight in beauty, the passion for justice ........are the workings
within us of a higher nature which has not been developed by means of
a struggle for material existence". Mivart also finds it inconceivable
that natural selection could produce "from the sensation of pleasure
and pain experienced by brutes, a higher degree of morality than was useful"
.[ In this respect he like Wallace is dissident towards the biblical teachings
of original sin.] Instead he proclaims that the germs of human morality
do not exist in primitive animals and is therefore evident in humans as
a result of some higher process than natural selection, while Wallace
accedes to its existence to some extent in lower animals but regards its
elation to the height of human morality, as proof of a spiritual mechanism
at work. Unlike Darwin, they are both contentious towards the skepticism
of the Sophists who regard moral values as merely human convention. They
conjecture that there is no natural selection for morality and as Mivart
puts it "no stream can run higher than its source" implying
that even if the usefulness criteria of evolution has developed into what
is today regarded as morally righteous " we see that the very fact
of an act not being beneficial to us makes it more praiseworthy"
thus dispelling the utility of formal morality. Unlike Wallace he regarded
the maternal morality exhibited by animals as being disparate to the formal
morality of human beings and that natural selection alone is unable to
bridge the gap.
They both relate to the three phases or modes of existence viz. inorganic
(unconscious), organic (conscious) and spiritual (intellect) or in Mivart
case the physical, hyperphysical and supernatural and both relate to the
belief that an almighty force is involved in their transformation or interaction.
Wallace states "These three distinct stages of progress from the
organic world of matter and motion up to man, point clearly to an unseen
universe -- to a world of spirit." Mivart also concludes "there
is and can be absolutely nothing in the physical sciences that forbids
[us] to regard these natural laws as acting with divine concurrence"
although he only vaguely speculates as to the underlying ontology behind
the "subordinate action of natural selection."
To summarise therefore, both advocate evolution and each aspire to a
reconciliation between Darwinism and their own
personal beliefs. Whereas Wallace demonstrates the inapplicable use of
natural selection regarding mankind's intellectual growth, Mivart projects
the technical defects of Darwin's theory and its inability to coherently
account for the differences in related but separate species. However they
both rely upon ethical arguments to reinforce their position and claim
that human personality has not developed by means of natural selection,
since many attributes occur very rarely and are not related to survival.
Mivart's religious beliefs upon creation and those spiritual convictions
held by Wallace are centred upon a teleological view which contends Darwin's
monopoly of evolution and his explanation of all life on Earth as being
" products of the blind eternal forces of the Universe."
Idealism and Realism
in Physics
It is often said that the Holy Grail of physics is to find a single equation
that can explain the whole of physical phenomena - an equation that can
be written across a T-shirt. The fact that the world's greatest minds
have been unable to achieve this is a testament as to how complex this
mathematical structure must be - if such an equation actually exists.
However, we can at least begin to speculate upon the nature of any such
equation.
The equations that are already known to accurately describe fundamental
physical laws are rather esoteric, while those theories that are yet more
ambitious (and speculative) employ concepts that are even further removed
from everyday experience. String theory for example, replaces the geometry
of points with that of extended one-dimensional objects and with its 2nd
Revolution (M-Theory), employs higher dimensional p-branes. These all
require invoking extra dimensions of spaces that become compactified under
symmetry breaking. Supersymmetry, requires the introduction of (anti-commuting)
grassman variables in order to produce 'unreal' fermionic dimensions (which
are measured in supernumbers), in addition to the real (bosonic) dimensions.
An alternative strategy for a Theory Of Everything (TOE) is Twister theory,
which is based on spinor mathematics and relies greatly on sheaf cohomology,
neither of which bears any resemblance to Euclidean space. So how are
we to interpret the underlying nature of any theories written in such
abstract mathematics?
We could possibly gain something from Plato's perspective. He believed
that there were three distinct worlds, namely the Physical (real) world,
the Spiritual world and the Ideal world - the latter being the more superior.
The Ideal world is (as its name implies) perfect and contained for example
exact circles, to which only approximate copies exist in the Physical
world. The whole of Euclidean geometry (the main branch of maths in those
days) relied on constructions using only the circle and straight line.
[The three great-unsolved mathematical problems of antiquity, namely the
squaring of the circle, the trisection of an angle and the doubling of
a cube, were examples of the limitation of these two particular Platonic
tools. It was another two millennia before Galois theory showed the impossibility
of these quests.]
In some ways maybe the new fundamental theories should be regarded as
being of a Platonic Ideal, rather than physically real. Indeed quantum
theory describes the world in terms of complex wave functions, from which
we extract physical observables (eigenvalues) by means of hermitian operators.
Complex numbers have an imaginary component and we do not therefore attach
physical reality to the wave function itself (which only represents a
probability amplitude). But what about strings and higher dimensions?
Two great equations of the early part of the last century were Einstein's
field equation in General Relativity and Dirac's equation in Quantum Theory.
[Both these pass the T-shirt test, although their solutions are often
lengthy] One of the significant features that they share is that they
are both coordinate free. In other words we can accept the equations as
accurately predicting the physical world but there is no special privilege
given to any particular coordinate system in which they are expressed.
The equations are like perfect sculptures over which we could draw any
contour lines, non of which would be as important as the statue itself.
The tensor nature of the former does not give uniqueness to an observer's
space and time. Likewise, the contact transformation which forced Dirac's
to produce his acclaimed equation, also removes the importance of any
particular reference system. It suggests that the underlying nature of
these theories exist in a Platonic context and that it is their particular
(and often inexact) solutions what we experience in our real (material)
world
Even the solutions that these equations give can seem bizarre, although
many have been tested to be true. Dirac's equation correctly predicted
antimatter and the fact that an electron rotated through 360 degrees would
become inverted, while the so-called twin paradox [sic] in special relativity
has also been demonstrated. In general relativity the Cosmological Principle
is invoked in order to find a possible description for the universe at
large i.e. the universe is assumed to be isotropic and homogeneous. This
produces solutions that depend upon the present mass density, which if
sufficiently large (Omega value greater than unity) would produce a closed
universe which although finite in size is unbounded. However if the total
value of Omega* is less than unity the universe will be open and negatively
curved (every point will in space be a saddle point - impossible to visualise
but otherwise quite acceptable). However what I do find uneasy is that
this implies an infinite mass, which must accompany the infinite space
of a universe, that has existed since the big bang and has been continually
expanding into-- infinity!!! [I am not aware of this specific issue being
adequately addressed, maybe some readers can provide enlightenment.].
The situation is somewhat reminiscent of Cantor's Transfinite numbers,
but the insight of pure mathematics into the Ideal world is one thing,
while the reality of the physical (material) world is another.
In summary, although such equations are of primary importance, they may
appear to exist in a Platonic Ideal world (which allows such peculiar
constructs), while their solutions are manifest in the physical world.
Any attempt to give physical reality to such structures as strings, twisters
and supermanifolds, seem to me to be ill fated. The philosophy of Idealism
may not appeal to many pragmatic scientists but as the mathematics that
underlies physical theories becomes more abstract and aloof, I feel it
is perhaps the most suitable viewpoint.
*Aside
It is believed by many that the value of Omega is actually unity, since
this avoids the above problem, while Hawking's work on quantum cosmology
relies upon the universe being closed. Theoretical reasons therefore need
to be given for such an unlikely balancing act, as well as an explanation
for the apparent missing mass. Recent proposals suggest values for a cosmological
constant that would significantly lower the required density of matter
and explain the observed '5th force' of repulsion that is volume dependent
. [However the introduction of a cosmological constant, may ruin essential
symmetries in string theory.]
Indeed some theories invoke a cosmological constant that was initially
very large and has decreased continually as the universe expanded. This
has the benefit of removing the need for inflation that accompanied the
spontaneous breaking of the Higgs field (a mechanism responsible for separating
the strong force from the electo-weak force during the very early universe).
It does however require the speed of light to become progressively reduced
during this expansion and for the possibility of successive universes
being seeded within one another producing a fractal structure! Recent
observations on distant galaxies seem to suggest that the coupling constants
of the fundamental forces have indeed changed over the history of the
universe, which would imply that the laws of physics have not remained
the constant as the universe expanded (for example the mass of the proton
and neutron would have been different in the distant past).
******************
Since my previous article (Idealism and Realism in Physics), I have
become aware of recent developments concerning our understanding of the
big bang in relation to M theory. The raison de etre of M theory is that
by adding an extra dimension, we find that the 5 contending string theories
(and supersymmetry) become a network of equivalent mathematical models
when viewed from this 11 dimensional manifold. Our universe is then explained
in terms of 2 dimensional membranes (rather than 1dimensional strings)
and other higher dimensional manifolds (unfortunately termed p-branes)
are also possible. New developments in M theory invoke parallel membranes,
which help explain several intriguing phenomena, such as the weakness
of the gravitational interaction [Gravity is viewed as emanating from
this parallel membrane into the 11 dimensional manifold and since we only
experience its effect in our 4 dimensions of space time, its strength
is greatly diluted.] Of particular importance is the recent discovery
that the big bang itself may be explained in terms of the collision of
2 such membranes. This allows us to avoid the embarrassment of the singularity
at the instant of creation and allows us to talk meaningfully about physics
before the big bang.
In some ways these new developments seems to undermine the viewpoint of
my previous article, since these parallel membranes and higher dimensional
p branes, are supposed to have existed before our physical universe and
could therefore be considered as more real! Indeed an infinity of universes
similar to our own but subtly different, are also believed to co-exist.
[This however is in a different context to the 'many worlds' interpretation
of basic quantum mechanics but both invoke the concept of a multiverse].
Even other more exotic universes are allowed (corresponding to higher
dimensional p branes), in which the laws of physics are completely different
from our own. My view however, is that although they provide exiting possibilities,
what is actually being discovered is the properties of a new 21st Century
mathematics, which may or may not refer to the real universe. Also even
if it does provide a Theory Of Everything, it does not mean that because
it predicts the possibility of other universes that they must actually
exist.
By means of a simple analogy, the graph of the quadratic equation y =
x^2 +1 does not actually cut the X-axis and therefore does not have any
real solutions for when y = 0 but does have imaginary solutions of x =+-i
. We can therefore talk meaningfully of the mathematical properties of
the roots even though the intersection of the graph with the X-axis does
not actually exist. Likewise there is a danger of assuming that these
visualised membranes physically exist, which may or may not be the case.
If one takes the Positivist outlook of Bohr and Hawkings then the importance
of a physical theory lies in its ability to accurately describe the universe
and one cannot speculate as to the ontology behind the theory.
A, B, OR C ?
Although Newton's inverse square law became the first formulation of a
gravitational force, it is not the only classical description of gravity.
For example we could express the gravitational law in terms of a field
in which each point in space could be allocated a gravitational potential.
Alternatively we could predict the motion of a body by utilizing the Maupertuis
Principle of Stationary Action (analogous to Fermat's principle of Stationary
Time regarding geometric optics). Each of these descriptions is equally
correct mathematically but describes gravity from 3 different viewpoints.
The advent of 'Modern' physics arose out of the revolutionary concepts
of relativity and quantum theory. Relativity theory can also be viewed
in three equivalent ways. From a kinematic analysis, by accepting an ultimate
limit to the speed of communication in order to justify causality, we
are forced to re-evaluate our understanding of simultaneity and hence
also time, length, and mass. Historically, Einstein realized the conflict
between Newtonian mechanics and Maxwell's laws of electromagnetism and
developed the special theory by boldly overthrowing the former. A third
method of approach would be to start with the postulate that matter and
energy are intrinsically the same. Consequently as we increase the kinetic
energy of an object its mass increases (relative to us) and this again
leads up to the scenario of relativity.
Whereas the old quantum theory was born out of Planck's postulate that
energy could only be radiated in discrete amounts, the new quantum theory
(especially field theory) has its roots formulated around Heisenberg's
Uncertainty Principle. It became evident that the four dimensional quantity
termed 'action' was discontinuous and to speak of any quantity smaller
than Planck's quantum of action was meaningless. Again we can look at
three different viewpoints in order to develop our model but this time
they are not all equivalent
Firstly we could take Einstein's interpretation which accepts that there
is a fundamentally lower limit to the accuracy with which we can make
'incompatible' measurements (e.g. energy and time) but that there is an
objective reality beyond these limitations even though it cannot be perceived
directly. The statistical nature of the wave function ('psi'), in his
view, merely expressed the indeterminate aspect of the apparatus interacting
with the object and did not doubt the absolute reality of the object.
Alternatively we could also in the Uncertainty Principle by postulating
that although there is a hidden reality to an object, there is also an
inherent tendency for all objects to fluctuate in their paths within the
quantum of action, thus giving it an undulating uncertainty. The Maupertuis
Principle would then be an approximation to particle propagation, in the
same way that Fermat's Principle is an approximation for light (neither
of them is applicable to wave phenomenon). Just as General Relativity
refines classical gravity, so Quantum Theory refines the Maupertuis Principle.
Thirdly there is the orthodox (Copenhagen) view, that all we can be sure
of are observable values and that the subject is inexorably interwoven
with the object. In other words there is no objective reality beyond the
constraints of our measurements and the way in which we carry out our
observations affects the reality of an object. It is therefore meaningless
to ask whether an electron is a particle or a wave. Einstein once asked
a friend if he really believed the moon only existed when he looked at
it. Ironically his mentor Ernst Mach regarded science as merely an "economy
of thought"; all we can ever do is make observations but not complete
explanations regarding ontology. Science to him was nothing more than
empirical facts grouped together under uniformity and conservation laws.
Each of the viewpoints support the Uncertainty Principle but there is
a profound difference in their implications. The first two interpretations,
which allow varying degrees of objectivity, do not stand up to recent
experimental evidence (c.f. John Bell's Inequality and Alain Aspects experiment).
Instead it seems that 'knowing' has an almost mystical effect on the universe
at the microscopic level. Just as mind is the ghost of the body, the quantum
has become the ghost of the atom. Current understanding seems to indicate
a deeper meaning to the concept of relativity, in which knowledge is not
absolute but conditioned by standpoint and circumstance. Sages of ancient
India taught that the mind is the centre of the Universe but whereas modern
psychologists tend to use a reductionism approach to the mind, modern
physicists are seriously contemplating an holistic approach, reminiscent
of Taoism, forced upon them by the outcome of Quantum Theory. [ Bohr adopted
the Yin Yang symbol for his coat of arms!]
As a consequence of the apparent validity of the orthodox interpretation
of Quantum, we unavoidably return to the dilemma of 'instantaneous action
at a distance' - that which Einstein was happy to ameliorate with his
General Theory of Relativity.
Interestingly in the limit of "c" approaching infinity, Einstein's
equation approaches the Newtonian prediction of an inverse square law
and gravitational force is proportional to the product of the masses,
while in the limit of Planck's constant approaching zero, Quantum predictions
agree with classical theory. [Indeed it is the sameness of "h"
which make QT effects unobserved except on atomic scales and the largeness
of c which makes relativity effects unimportant in everyday circumstances]
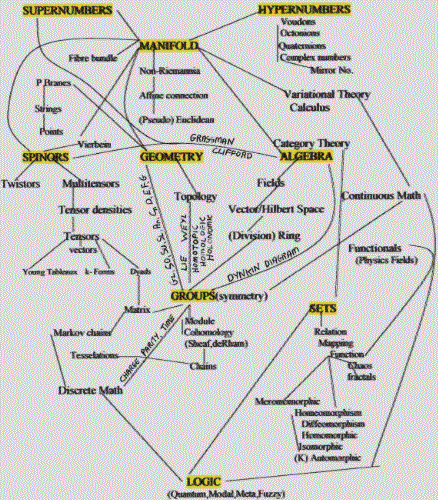
MATHEMATICS SPRAY DIAGRAM
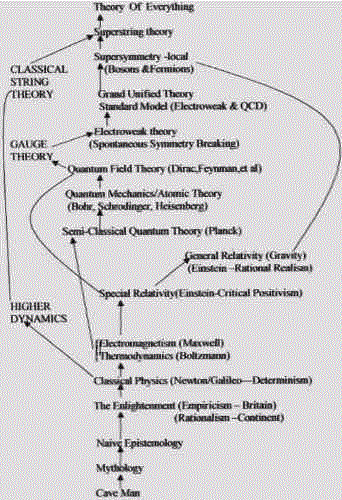
PHYSICS SPRAY DIAGRAM
INFINITY AND
THE MIND
"God created the Integers, all else is the work of
man"
L. Kronicker
GODEL'S INCOMPLETENESS THEOREMS
Preamble
Leibniz
considered if all proposition is decidable within logic
(i.e. completeness), while much later Hilbert asked if axiomatic logic
can be formalized in a consistent way.
Between 1910 and 1913 Russell and Whitehead produced the 3 volume Principia
Mathematica, in which they claimed to have reduced all of mathematics
to a unified system of axioms from which all theorems of mathematics could
be derived, just as Euclid had attempted to do for geometry. Hilbert however
was skeptical and challenged mathematicians to prove rigorously that Russell
and Whitehead's program had succeeded.. This question was settled in 1931
by the theorems of Kurt Godel, who demonstrated that in a system of sufficient
complexity, such as the theory of numbers, there must exist statements
that cannot be proved either true or false. [As a corollary there must
also be true statements hat cannot be proved].Consider the following statement
"This theorem cannot be proved". If this statement is false,
then it can be proved so we have a contradiction i.e. an inconsistency.
However if the assertion is true we have a statement that cannot be proved,
hence incompleteness. Godel's theorem does something similar to this for
formalized systems such as arithmetic by using Godel numbers to encode
axiomatic statement. He allows statement and numbers to refer to themselves
and by a process of diagonalization allows statements that are true of
their own Godel number. Hence if we code that an arithmetical statement
similar to "This theorem cannot be proved" which refers to its
own Godel number we arrive either at a contradiction (if the statement
can be proved) or an incompleteness (if it cannot be proved the assertion
is true but cannot be proved). Turing also posed a problem on decidability
(called the Halting problem) , by considering a universal machine that
could run all programs (similar to today's PC's which can run on any valid
operating system). Now when you run a program, either it stops and spits
out an answer or it goes on for ever. He asked whether it would be possible
to decide in advance on whether a given problem could be solved
by a particular program (set of algorithms) in a finite amount of time.
Turing showed that the Halting problem is undecidable. To do so
he played much the same game as Godel, by assuming that the halting problem
is decidable, Turing showed (c.f. proof below) that you could construct
a program that stops if and only if (IFF) it does not stop (this
contradiction therefore shows that the assumption is false). So Turing's
halting problem is a similar example of Godel's undecidability.
Godel achieved his numbering code as follows;
+ - * / ( ) = 1 2 3 4 5 6....x y z .......etc
corresponds to the following digits
1 2 3 4 5 6 7 8 9 10............etc
So to code a string of symbols such as
4+ 7=11
we form the number 2^12* 3^1* 5^15*7^7*11^9*13^9
where 2,3,5.7 is the sequence of primes and the
powers 12, 1, 15 ,7,9,9 are the codes of the symbols 4,+,7,=,1,1 of the
string
In this way we associate with each string a code
which will be a whole number. Thus if the code is 720 we can uniquely
factorise this as 720 = 2^4*3^2*5^1 and the symbols whose codes are 4,
2, 1 are / - + hence 720 is the code for the string / - +
Is the set of all
extraordinary sets, itself ordinary or extraordinary? This is Russell's
paradox which can be reframed in terms of a country in which each
library has an index of all its books. Some libraries also include the
actual index book itself (i.e.the index book is an ordinary set), while
in other libraries, the index book does not mention itself (an extraordinary
set). Now the national museum contains a master index
book, which lists all the index books of those libraries
that do not contain themselves (i.e. a list of
all the extraordinary sets). The question therefore arises
as to whether this master index book should contain its own title. If
it does not, then it cannot be said to contain all those
index books that do not contain themselves, whereas if it does contain
itself it cannot be an index only of books that do not
contain themselves? This discovery by Russell devalued 10 years of
Frege's work on the reduction of arithmetic to set theory.
Wittgenstein
said that a sentence cannot refer to itself; all sentence can do is say
what it means .The following are examples of self referential
sentences, which therefore lead to paradoxes. Similar 'strange loops'
can be found in Godel's incompleteness theorem, Richard's paradox, Cantor's
Paradox, Bach's fugues, Escher's drawings and in Turin's universal computer
(halting problem) and is present in Russell's criticism of Frege's set
theory (the set of all sets that do not contain themselves)
This
sentence is false {The liar's paradox of ancient Greece)
Is
this a question? {Yes, if this is an answer?}
If
a man says that he is a liar should you believe him?
The
word “long” is heterological
(since the word is actually short in length) whereas the word “short”
is not heterological (since the word “short” is short). Is the
word “heterological” itself heterological?
The
sentence below is true.
The
sentence above is false.
"The
least integer not describable using less than 19 syllables"
has only 18 syllables. (this is Berry's paradox)
"I
cannot imagine the world existing without me"
{A statement which illustrates the impossibility of perceiving personal
non existence}
Nostalgia
ain't what it used to be
Why
is there only one monopolies commission
Richard's
paradox assigns supposes a list of all real numbers between 0 and
1. It is then possible by a diagonal slash process to define a number
on the list (by taking the nth number on the new list to be one greater
than the nth digit of the nth number on the list). This new number however
is clearly a finite definition that would satisfy the condition for being
a member of the list and yet differ from every member of it.
Cantor
's diagonal theorem shows that any set has strictly more subsets than
it has members This leads to a paradox in that for an all inclusive infinite
set, every subset of such a set would be a member of it but due to his
diagonal theorem, every set has strictly more subsets than it has members;
there is thus no largest cardinal number. Cantor proved (using a diagonal
slash technique) that there are more real numbers between any two integers
than there are whole numbers. The infinite number of natural (whole numbers)
is called Aleph zero while the infinity of real numbers (including decimals
irrational numbers and transcendental numbers) is the cardinal c
= 2^Aleph zero. The continuum hypothesis asserts that c = Aleph one (i.e.
Aleph one = 2^Aleph zero, however Cohen has proved that this statement
is independent of the other axioms of set theory and we can add on the
axiom that the continuum hypothesis is true (or false) without making
the system inconsistent. Cantor also showed that there are more transcendental
numbers than rational numbers since if the number of Transcendental numbers
was also Aleph zero then the total number of reals would be Aleph zero
+Aleph zero =Aleph zero, which is false since we know that the number
of reals is c =2^Aleph zero> Aleph zero.
To
summarize, what Godel did in producing his First incompleteness theorem
was to find a statement G£ in the formal language of £ that
expresses the mathematical sentence "G£ is not provable from
£". In other words G is to represent the self referential sentence
"This sentence is not provable from £". Hence G£
must be true but not provable, since if it were false it leads to a contradiction,
so it must be true and therefore to be consistent, it asserts its own
unprovability. Godel achieved this in two steps; first he found a way
of assigning a code number to each sentence in the language of £
and then by a method of diagonalization he provided a way of making sentences
in the language of £ that refer to themselves. If we try to write
out G£ in English we get an infinite sentence: "£ cannot
prove that £ cannot cannot prove that £ cannot prove that
£ cannot prove that ...... . . . .In other words we say that G£
. . . IFF. . . .(£ cannot prove that G£). His second theorem
states that if we demand consistency then the theorem that states this
cannot be proved. Other central negative results of logic include Tarski's
theorem on the undefinability of truth (that arithmetical truth is not
arithmetically definable)and Church's theorem on the undecidability of
logic (that arithmetic is not decidable). Godel's theorems devalued much
of Russell's work, which tried to reduce arithmetic to logic (as initiated
in his Principia) and also showed Turin that his initial optimism of designing
an algorithmic machine that could decide if conjectures were true or false
(e.g. the 4 colour problem, Fermat's last theorem or Goldbach's conjecture)
was unattainable.
By
focusing on provability rather than on truth, Godel's sentence avoids
the absurdity of the liar's paradox (" this sentence is false").
If formal arithmetic is consistent, meaning that only true statements
can be proven, then Godel's statement must be true. If it were false then
it could be proven, contrary to the consistency! Furthermore it cannot
be proven, because that would demonstrate just the opposite of what it
asserts, its unprovability. Moreover Godel showed that if the consistency
of the formal system could be demonstrated inside the system itself, then
the informal argument just given could be formalized and the formalized
version of the statement " THIS STATEMENT IS UNPROVABLE" would
itself be proven, thereby contradicting itself and demonstrating the inconsistency
of the system.
First Theorem
There is no consistent, complete, axiomatizable extension of Q. (Q
being the Peano 'arithmetical' axiom system)
In other word Godel became famous for proving that you couldn't prove
everything that is true, even in such an apparently simple subject as
arithmetic. In effect, he showed that, it is not possible to prove
that all true statements in arithmetic can be proved (even its own consistency).
Let £ be an axiomatic set theory that is a normalization of an
ordinary arithmetic A. Inside S we have symbols from which we construct
strings and the axioms of S tell us how we are to manipulate
strings. Hence 2+2=4 is both a formula in A and a string in S.
In particular strings that involve a numerical variables 'n' are termed
signs. Now every sign can be labeled by a Godel number that
are arranged in order, and let R(n) is the nth sign. Hence every
sign is equal to some R(n) for a suitable choice of n.
Let [R(n),n] represent the string which substitutes a variable n into
the sign labeled R(n). Now if it is NOT possible to prove the string
[R(n),n] in £, for a particular value of n, then we include it in
a Cantor set K. For example the string n + 6 =0 is not provable for n=2
so n is an element of K.
The statement, S that a particular value of n is a member of K, can itself
be given a Godel number . Now, by a process known as diagonalization**,
it is possible for a Godel number to represent a statement that
is true of its own Godel number!!! [Diagonalization of a A will be a
sentence that says that A is true of its own Godel number-
or more precisely, the diagonalization will be true IFF (if and only if)
A is true (in £) of its own Godel number. So [R(n),n] can be a statement
labeled R(n) which is about S as implied by the ~ provability of [R(n),n]
where ~ means negative (of provability). Hence this statement R(n) can
be about the Godel number R(n) itself! With this particular situation,
if we consider the string [R(n), n] it can be shown that it is not provable
in £ but also it will be shown that NOT [R(n),n] is also not provable,
in other words it is undecideable. To summarise, R(n) can be a statement
which states the fact that the non provability of a string means
that the particular number it refers to then becomes a member of a set.
The paradox then arises when we let that be true for the Godel number
R(n) itself (i.e. the Godel code for the sign itself becomes the number
for which the statement is true).
**(This is reminiscent of that introduced
by Cantor in his theory of transfinite numbers, in which a new number
is obtained from a diagonalization technique and this can then be introduced
into the set, ad infinitum)
Godel number
. . . . . . . . . . . . . . . . Axiomatic
Set theory
G(n) . . . . . . .. . . . . . . . . . .
.. . . Statement about a number (which might be
true(provable) or false depending on the number)
Note that [G(n),n] represents the string associated with a Godel number
G(n).
. . . . . . . . . . . . . . . (Sign S).. = ..n
is an element of set K and if ~Prov[G(n),n] (i.e.if G(n) cannot be proved
for n)
Diagonalization is a process which says of a sign S that "S is
true of its own godel number", or more precisely, the diagonalization
will be true IFF (if and only if) S is true of its own Godel number. Hence
we could code any statement and give it a corresponding Godel number
and then decide if the statement would still be true if the variable
were replaced by its own Godel number; if so then we have successfully
diagonalized the statement and we can express this fact by labeling it
with the originall Godel number. Let (by the process of diagonalization),
the Godel number R(n) now represents a statement that is true of its own
Godel number i.e. we represent Sign S by the Godel number R(n) and obtain;
R(n).. . . . . . . . . . . . . . . . . ..
.S . = .Statement
that n is an element of set K as implied by ~Prov [R(n),n]
[
It therefore seems legitimate to ask whether the (new) statement, which
is represented by [R(n),n], is true, in other words can we prove [R(n),n].
We then can provide the following proof of incompleteness;
Proof. Consider the following signs;
:[R(n),n] ................{1}
not-[R(n),n]...........{2}
If {1} can be proved then it means that n is a member of K, which
because of diagonalization, implies (by definition of K), that {1} is
not provable for some n -- hence {1} asserts its own unprovability.
However neither is statement {1} disprovable, since if the
negative of {1} (which is written in statement {2}), is provable, this
implies the negative of 'being a member of K' in other words n
is not a member of K. Because of diagonalization, this in turn means that
[R(n),n] is provable for some of n, which contradicts (2) and since £
is assumed consistent it follows that {2} is not provable in £.
Hence the assumption that the negative of {1} is provable is false and
therefore {1} is neither provable or disprovable. i.e. it is undecidable!
The statement [R(n),n] can therefore be regarded as asserting its own
unprovability. Hence in mathematics we have to abandon the dream of being
able to create a machine that will operate a computer program capable
of churning out theorems which have been proved to be true. Instead we
have to rely on the ingenuity and creativity of mathematicians to decide
upon the validity of Fermat's last theorem or the four colour problem.
[Note that {1} cannot be false since as we have just shown, that would
means that R(n) can be proved and hence{1} is true, which is a
contradiction, so we are left with the alternative that {1} is true
which means that R(n) cannot be false since that would be a contradiction,
in other words R(n) must be true. Also note that{1} is true
if it cannot be proved, hence we arrive at the only alternative,
that R(n) can be true if it is not provable.
To recapitulate, by coding axiomatic statements in terms of Godel numbers,
we allow the possibility of numbers expressing statements about themselves.
For example if a statement is made about a number, this statement is itself
designated as a Godel number and the possibility then arises that this
statement represented by the number, refers to the number itself. We can
test the provability of the Godel number that represents a given statement
about a specific value of a variable (e.g. 2 + x =7; if x=9 ) and in particular
(by means of diagonalization), a Godel number can refer to a string which
is true of its own Godel number. A Godel number can then be given to a
statement that relates to a negative outcome of another statement (i.e.
unprovability, as in relation to set K), which is coded by the same
Godel number, and we can then demonstrate the unprovability of the overall
statement. In summary we have constructed a string viz. [R(n),n] that
expresses its own unprovability! Hence in any formal system we will have
theorems, which although true, are not provable within the systems and
even if we amend the axioms and enlarge the system so as to be able to
encapsulate these known theorems, this very act will produce more unprovable
theorems! Some people have speculated beyond this precise formalism
to less rigorous systems, such as the human Genome. For example there
certain degenerate diseases that a given human phenotype is prone to,
but some would suggest that even if we identify the aberrant genes and
make alterations to the Genome that guarantees immunity to particular
ailments, this very act will itself ensure that other (new) self destructive
biological effects would become extant. To continue this analogy, we can
regard systems as record players which work well for most records but
the very design of the player means that there is always a record that
when played, will cause the player to self-destruct. However any modification
to the player's system that prevents this happening with such a record,
will automatically produce changes that will ensure that it is capable
of being destroyed by another, as yet unknown record (and so on ad infinitum).
For example in the above, S is the statement that n is an element of
a set K when ~Prov[R(n),n]. Now if we let S be given the Godel number
R(n) we can show that the statement [R(n),n] cannot be proved since this
would imply that there is a number that is a member of the set K which
in turn implies a Godel number, that itself asserts that the statement
[R(n),n] cannot be proved, so we arrive at a statement that asserts its
own unprovability!. What's more we cannot disprove the statement, since
by asserting the negative statement, it implies that n is not a member
of K and this in turn means that R(n) is provable for some of n, which
contradicts the negative of the statement viz ~[R(n),n]. Hence the assumption
that ~[R(n),n] is provable is false and therefore [R(n),n] is neither
provable or disprovable. i.e. it is undecidable!
More formally Godel's First theorem can be expressed as follows;
Definitions:
1. Diagonalization
If A is a formula in the language of arithmetic that contains just the
variable x free then the diagonalization of A will be a sentence
that says that 'A is true of its own Godel number', or more precisely,
the diagonalization will be true IFF (if and only if) A is true
of its own Godel number.
2. Provability
Prov£[m,n] is true if and only if
(IFF) m codes up a proof from £ of the sentence coded up by n.(i.e.
m proves n)
3. CON(£) . . . . means that £ is consistent
The First incompleteness theorem is proved by finding a sentence G£
in £ that expresses the mathematical sentence "G£ is
not provable from £". . G£ must therefore be true but
not provable. [The reason is that if this statement
can be proved true, we have a contradiction i.e an inconsistency. However
if it cannot be proved, the assertion is true but cannot be proved, hence
incompleteness].
** .
G £ ... . . . ... . ..if and only if... . . .. ..... .~E(m)[Prov£[m,<G£>]
. . . . . . . . . . . . . .{1}
Note that if {1} is false then we obtain the
statement E(m)[Prov£[m,<G£>] is true.
We will now demonstrate that when the above statement
is true there is no proof that codes for the statement i.e. G£ asserts
its own unprovability..
G£ states that no natural numbers m of a
certain kind exist (namely those that code a proof for <G£>),
so it seems legitimate to ask whether G£ is a true or false statement
about the natural numbers. Note that G$ is true if it is not provable
from £, so it seems that either G£ is true
and not provable by £. or that G£. is false
and provable by £. Now if we assume that £ is consistent,
then we can rule out the second option and conclude that G£ is true
but not provable in £, which is Godel's First Incompleteness Theorem.
[If there were a proof of G£, then the meaning of the statement
that G£ actually asserts, namely that there is no proof, would be
false, so G£ would have to be false as an arithmetical proposition
which implies that our formal system is so inconsistent as to allow false
propositions to be proved. Thus it must be true that there is no proof
of G£, which is exactly what G£ is stating, hence we have
a true statement which has no proof within the system. Also since we have
just established that G£ is true, then ~G£ must be false and
therefore we cannot prove ~G£ to be true, otherwise we will again
have a system that proves false propositions]
We have therefore created a particular self referential
statement that, in order to be consistent, cannot be proved and hence
the statement that ' it cannot be proved ' is true
but in turn cannot be proved. So in order to have consistency G£
has to be true, but G£ states that the statement about itself cannot
be proved, which is true and so we have a statement that says of itself
that it is not provable even though it is true. In other words if G£
is true, it implies that G£ is not provable for some m, hence it
asserts its own unprovability. Therefore we cannot prove something
that is known to be true (namely the statement that proclaims that this
diagonalization is not provable). [If G£ can be proved
false, then not G£ is provable, which means that G£
is provable for some m, which is a contradiction and we therefore lose
consistency.] Hence there are certain statements in arithmetic that cannot
be proved nor disproved i.e. they are undecidable! So if we insist on
consistency then we must have incompleteness but if we try to demand completeness
we cannot have consistency. As we shall see below, an example of G£
is the statement that £ is consistent i.e. CON(£) as this
leads to the conclusion that £ is consistent only if it is not provable,
which is Godel's Second Incompleteness theorem
Note that {1}cannot be false since as we
have just shown, that would mean that G£ can be proved for
some m and hence {1} is true, which is a
contradiction, hence we are left with the alternative that {1}
namely ~E(m)[Prov£[m,<G£>]
is true, which means that G£ cannot be false
since that would be a contradiction, in other words G£ must be true..
Also note that{1} is true if it cannot
be proved, hence we arrive at the only alternative, that G£
can be true if it is not provable Statement {1}
is an assertion that diagonalisation (which is assumed true by its definition),
when applied to a particular (true) statement regarding its own provability,
is not provable, in other words we have a truth that cannot be proved.
It is therefore true that we cannot prove that this diagonalization
is provable, in other words we have a truth that cannot be proved. [If
we state that this particular diagonalization is possible to prove i.e.
the negation of {1}then we arrive at a contradiction.]
Hence the statement that says that "its own diagonalization cannot
be proved" is true but undecidable i.e. it cannot be proved nor disprove.
If we try to write out G£ in English we get an infinite sentence:
"£ cannot prove that £ cannot cannot prove that £
cannot prove that £ cannot prove that ...... . . . .In other words
we say that G£ . . . IFF. . . .(£ cannot prove that G£).
. Second Theorem
If Z is consistent then the statement
that says this is not a theorem of Z ( In other words Z cannot prove its
own consistency, or £ is consistent if and only if £ cannot
prove CONsistency(£). Z being the axiomatic system of arithmetic)
Let T be the string [R(n),n] which as we have just shown asserts its
own unprovability, and let Z be any formula in £ which asserts the
consistency of £. We therefore want to prove that Z cannot be proved
in £. Godel's first theorem reads 'if £ is consistent
then, then T is not provable in £'. We can therefore express
this in £ as:
'£ is consistent' in our formula Z
'T is not provable in £' is just T itself, because T asserts
its own unprovability, so Godel's first theorem written in £ takes
the form of
Z implies T .........i.e '£ is consistent implies T is not provable
in £'
If we could prove Z in £ then this would enable us to prove
T. However we know that T cannot be proved, hence Z cannot. Since Z asserts
the consistency of £, it is not possible to prove Z consistent within
£, which is his second theorem. [The consistency of £ could
be an example of Godel's First theorem, since even if £ is consistent
it is not provable i.e. R(n) (or its equivalent G£) above, becomes
CON(£) which asserts its own unprovability].
Alternatively stated, we know that if £ is consistent then T is
true. In this way we can show that there is a proof from £ of CON
(£) implies T. Now if £ could prove CON (£)
as well, then we could apply Modus Ponens and obtain a proof from
£ of T, which is impossible (since T asserts its own unprovability).
Therefore £ cannot prove CON(£). The main point is that such
axiomatic systems cannot prove their own consistency without having to
'step out of the system' and if we do this, how do we know that this system
in turn is consistent, unless we again move to a higher system in order
to check its consistency and so on ad infinitum. Likewise in Godel's First
theorem, if we produce a sufficiently rich system of axioms, there will
always be true statements within that system that cannot be proved and
whatsmore, if we identify these statements and add suitable axioms that
will ensure that these can now be proved, then we will inadvertantly introduce
new true theorems, that in turn are undecidableand and so on .
. ..Some people use this to 'prove' that we will never completely understand
the universe because we are part of it (some cite Heisenberg, uncertainty
as an example of this) or that we cannot completely understand the mind
(and therefore our thinking/theories will be limited) because we cannot
step outside of it. However Godel's theorems do not necessary relate to
such ideas and indeed it can be shown that some smaller formal systems
such as the axioms of geometry are consistent [These axioms are not sufficient
to produce a complete system of arithmetic for example, however the integers
without the operation of multiplication can be consistently formalized
but the system is then restricted i.e.incomplete]. Godels theorem may
have some bearing on Law however, in that it demonstrates that it is not
possible to have a legal system that is guaranteed to dispense the law
in a way that is instinctively just at all times (in other words we need
a judge to intuitively interpret given situations). Hence given a particular
system of law (which itself varies considerably throughout the world),
it is always possible to find a scenario that will lead to a verdict that
would intuitively appear to be unjust. [We often attempt to override
these occurrences by appealing to another, usually higher court, but as
already emphasized, the consistency of even this may be questionable]
In the same way that quantum mechanics provided limitations on what we
could demand regarding determinism, Godel's theorem demonstrates the limits
of formalism. Indeed Einstein's theory of general relativity contains
its own incompleteness in that it predicts the inevitability of a singularity
(where its own laws of physics break down) at the centre of a black hole
for a collapsing star beyond a certain mass.
It is difficult to actually find interesting, examples of undecidable
statements but a good candidate is known as "P = NP", which
asks whether every class NP question is actually class P. in other words,
if an answer to a question can be checked in polynomial time, can
it always be found in polynomial time. At first sight the answer to P
= NP seems to be no, since finding an answer to something ought to be
harder than checking it once someone has found it. Yet nobody has been
able to prove or disprove it, and it may in fact be undecidable
Transfinite Numbers
Suppose we make a list of all real numbers
between 0 and 1. It is then possible by a diagonal slash process to define
a number that is not on the list (by taking the nth number on the new
list to be one greater than the nth digit of the nth number on the list
cf. example below*). This new number however
is clearly a finite definition that would satisfy the condition for being
a member of the list and yet differ from every member of it. Using this
diagonal slash technique Cantor proved that there are more real numbers
(R) between any two integers (Z) than there are whole numbers. The infinite
number of natural (whole numbers) he called Aleph zero, while the infinity
of real numbers (including decimals irrational numbers and transcendental
numbers) is the cardinal c = 2^Aleph zero (which from Cantors diagonal
theorem below, is greater than Aleph zero itself).*
The continuum hypothesis asserts that c = Aleph one (i.e. Aleph
one = 2^Aleph zero), however Cohen has proved that this statement is independent
of the other axioms of set theory and we can add on the axiom that the
continuum hypothesis is true (or false) without making the system inconsistent.
More generally, Cantor suggested the Generalized Continuum Hypothesis
in which for all values of x, 2^Aleph x = Aleph x+1.
Aleph 0 is therefore the lowest infinity (transfinite
number) and is associated with the natural numbers N
The number of even numbers is also Aleph 0 as is
the number of odd numbers, since both these sets can be put into one-to-one
correspondence with each other, so;
Aleph 0 + Aleph 0 = Aleph 0
Also, Aleph 0*Aleph 0 = Aleph 0 . . . . (since
the cartesian cross product of the two can be placed in a grid, each unit
of which contains a pair of numbers that can be put into one-to-one correspondence
with the same size grid labeled with the natural numbers. By moving around
the grid in a cyclic manner, if we keep filling in the pairs of numbers
in the first grid and a corresponding natural whole number in the second
grid, we will just fill in the upper right hand quarter of each infinite
grid ).
Now the cardinality of the real line is c = 2^Aleph
0. We can therefore assert that the cardinality of the number of points
on a plane is c*c = 2^Aleph 0*2^Aleph 0 = 2^Aleph 0 +Aleph 0 = 2^Aleph
0 = c , and likewise the cardinality of the number of points in a 3 dimensional
space is also just c =2^Aleph 0
Cantor 's diagonal theorem shows that any set has
strictly more subsets than it has members. The number of subsets (including
the null set and the whole set is equal to 2 ^k where k is the number
of members. [This can be obtained by considering that each subset is one
of a combinatorial series kC0, kC1, kC2 .....kCk and that these form a
typical Pascal triangle in the binomial series, whose sum of the coefficients
in each line are 2^k. viz. 4, then 8 then 16 etc,for the binomial expansions
of squared cubed and quartic etc. More generally if we have C choices
of colour and k elements, we obviously have C^k combinations of colouring
each element and if we limit this to just black and white, - where black
represents an omission - we obtain a total of 2^k possible 'subset' combinations].
Cantor then showed using a diagonal method shown below**,
that k is always less than 2^k even for infinite sets. This leads to a
paradox in that for an all inclusive infinite set, every subset
of such a set would be a member of it, but due to his diagonal theorem,
every set has strictly more subsets than it has members; there is thus
no largest cardinal number.
*The proof that the cardinality of the real
line is 2^aleph zero, is obtained by considering subdividing the unit
length real line into 2 an infinite number of times, so as to obtain a
small enough interval of [0,1] namely 1/2^n . We need to carry out this
an infinite number of times, in order to home in on an actual real number,
hence the cardinality of c is 2^ Aleph zero
**The proof that k<
2^k is obtained by arranging k sets of (1,0) and by choosing one member
in turn from each of the k sets, so as to produce a series of new sets
Sn, each containing k members which are either 1's or 0's. For example
consider the following list of Sn sets
S0 =<1,0,0,0,0,0,0,0.....>
S1 =<1,0,0,1,1,0,1,0,.....>
S2= <0,1,1,1,0,1,1,1,.....>
etc, etc down to Sk, so that the width
of the sequence of horizontal 0's and 1's is equal to k which is also
the height of the vertical column i.e. we have 'k rows and k columns'.
So the numbers of s rows equals k, while the number of combinations of
0's and 1's (which also has k members) must be 2^k ( since we have a choice
of two digits from each k set). Now by employing the diagonal slash technique
we alter each of the diagonal numbers highlighted in red (1 becomes 0
and 0 becomes 1). This ensures that we obtain a new sequence since the
first member will be different from that of S1, the second member will
be different from that of S2 and so on. Hence we have demonstrated that
there are members of the set described by 2^k that are not counted within
the list k i.e. k < 2^k even for infinite sets
Cantor also showed that there are more transcendental
numbers than rational (and algebraic) numbers. The proof resides in the
construction of a function h(f) which is defined as the height of a polynomial
f(t), being equal to the sum of the moduli of all the (integer) coefficients
of f(t)
so for f(t) =a0+ . + . + ant^n . . . . . . .This
defines t as an algebraic number
h(f) =n+/a0\+/a1\+/a2\+/a3| . .etc.
Now there are h integers that are <=h, hence
the number of polynomials is <<h^h , Consequently, there is a finite
number of polynomials over the integers of given height h. In other words
each integer h is associated with a finite number of polynomials and hence
algebraic numbers - that is they are Z countable. Since we have proved
above that R is uncountable and we now find that the algebraic numbers
are countable then we have demonstrated that transcendental numbers exist!
Now if the number of Transcendental numbers
was also Aleph zero then the total number of reals would be algebraic
(countable ) numbers + transcendental numbers = Aleph zero +Aleph zero
=Aleph zero, which is false since we know that the number of reals is
c =2^Aleph zero> Aleph zero. In other words the number of transcendental
numbers must exceed the number of algebraic (e.g rational) numbers. [The
three great mathematical problems of antiquity viz. the trisection of
an angle, the doubling of a cube (the Delian problem), and the squaring
of the circle, are all impossible to achieve by compass and ruler and
the last of these relies upon 'pi' being a transcendental number and so
crown 3000 years of mathematical effort!]
It is easily proved that the square root of a prime
number is irrational (indeed one of the Pythagorians showed this for SqRt
2). More generally for a prime number p we can prove by contradiction
that SqRt p is irrational:
assume that SqRt p = a/b . . . . for some integers
a and b. For simplicity I will show this specifically for the prime 5
although this is valid for any prime just by substituting the 5 for the
variable p
hence 5b^2 = a^2 . . .which implies 5 is a factor
of a^2 (hence so is 25)
CASE 1
if a^2 is even, a is even which implies b is odd
a^2 = 5b^2 implies both are even
which implies b^2 is even
which implies b is even which is a contradiction!
. . .(a/b = even/even)
CASE 2
if a^2 is odd (it ends in a 5)
this implies a^2 = c x 5 x 5 . . .where c is an
odd square
so a^2 = =5b^2 = cx5x5 = 25c
so b^2 = 5c . . implies5 is a factor of b^2 (hence
so is 25)
so b^2 = d x 5 x 5
and a^2/b^2 = [c x 5 x5] /[d x 5 x 5]
hence a^2/b^2 = [SqRt c x 5]/ [SqRt d x5] . . .
which is a contradiction! . . . (where SqRt 5 = SqRt [c/d]
* * * *
NEXT what about the n^Rt [2], is it
possible for this to be rational. Assume that n^Rt 2 = a/b
then 2 = a^n/b^n
that is 2b^n = a^n
or b^n +b^n =a^n
But this would contradict Fermat's Last Theorem
(see below), which has recently been proved valid for n>2
Hence n^Rt2 is irrational. This approach also shows
that even for n=2 there are no Diophantine solutions such that a^2 +a^2
= b^2, for 2 integers a and b
Fermat's Last Theorem
The final piece in this proof was provided by Andrew
Wiles and can be summarized by the following developments. Assuming that
there was a Diophantine equation which did violate Fermat's theorem, it
was possible to recast such an equation, in a form known as an elliptical
equation (y^2 =x^3 +ax^2 +bx^ + c). It was then eventually shown
that such an equation could not be a modular form. Now the T-S conjecture
claims that all elliptical equations are modular form. Hence if
the T-S conjecture could be proved, then it must be true that such an
imagined equation cannot exist i.e. such an equation which violates Fermat's
theorem cannot exist. This T-S conjecture (or at least a portion of it
that was crucial to Fermat's theorem) was provided by Wiles.
Bennett's Theorem
For natural numbers n and integers b,a , the n
th Root of [(b/a)^n + 1] is irrational
The main thrust is in demonstrating that if the
n thRoot of any integer Q is rational, then n th Roots of (Q+_1) must
be irrational [In other words for any consecutive integers Q and Q+1,
it is not possible for both of these to have n th roots
that are both rational.numbers.]
IF the n th Root of [(b/a)^n + 1] is rational,
then so is n th Root[(b/a)^n + 1] x a
hence n th Root [a^n +b^n] = c/q
so a^n + b^n = (c/q)^n
and q^n x a^n + q^n x b^n = c^n
thus d^n + e^n = c^n, (where d=qa and e=bq), which
contradicts Fermats theorem which has recently been proved by Andrew Wiles.
Hence n th Root [(b/a)^n + 1] must be irrational
Now we have an infinite number of rational numbers
(a/b) which yield an infinite number of irrational numbers for each power
n. If we make 'n' to be one of the infinite number of primes, then we
can form an infinite series of irrational numbers each of which is a different
prime root of a rational number. [Using prime numbers is not necessary
but it does increase the chance of the number being transcendental rather
than just irrational]. From this set of cardinality aleph 0, we can obtain
by combination under addition, all the (irrational) subsets of the individual
irrational numbers. Now the cardinality of such subsets is 2^Aleph 0,
which is greater than aleph 0. Hence we have demonstrated that the cardinality
of ALL irrational numbers (including those that are transcendental) is
greater than that of all the rational numbers (which is only Aleph 0)
and is equal to the cardinality of the reals i.e. 2^Aleph 0. Most of these
irrational numbers will in fact also be transcendental, which also have
a cardinality of Aleph 0, since the number of algebraic numbers rational
+ irrational) is in fact only Aleph 0. This new set (whose elements are
formed as subsets, from a combination of the sum of the original irrational
numbers), provide a means of producing 'most' of the transcendental numbers,
but it is not apparent how we can distinguish these from the ordinary
irrational numbers (such as the original irrational elements).
In Summary;
Reals = 2^Aleph 0 (uncountable)
Integers = Aleph 0 (countable)
Irrational algebraic = Aleph 0 (countable)
Algebraic (rational + irrational) = Aleph 0 (countable)
Transcendental = 2^Aleph 0 (uncountable)
Irrational (algebraic + transcendental) = 2^Aleph
0 (uncountable)
If we denote the ordinality of the infinity
of the Natural numbers as w (corresponding to the cardinal value of aleph
zero), then we find that unlike finite numbers we no longer have commutivity
of the operations of arithmetic viz
. 1+ w = w . . . . . . . . but w + 1
= w + 1
2*w = 2+2+2+2+.... = w. . . .but w*2
= w + w . .i.e w*2 is two omegas placed next to each other, which gives
the ordinal w+w but2*w is omega twos placed next to each other which makes
an ordered set with ordinal number w!
We can proceed to higher ordinals such
as 0,1,2,3,w,w+1,w+2,w*2,w*2+1,w*2+2,w*w,w*w*w(i.e.^3), w^4, w^w What
about the first ordinal a such that w*a =a? well if we take w^w it is
evident that w*w^w changes nothing, so a=w^w. [In other words w*w^w=w^(w+1)
= w^w]. now the firs ordinal such that w^a =a is called epsilon zero e0,
which must have the following form w^w^w^w^w^w.. . . . . . . . evidently
putting such a symbol in the exponent position over an omega does not
change anything, since a stack of omegas 1+w high is the same as a stack
w high A better way of describing this is by the operation of tetration
(tetra for 4,since it is the next logical progression after add, multiply
and exponentiation); for example 4 tetration 2 means 2^(2^(2^2))=2^2^4=
2^16 =64,536 while 3 tetration10 is 10^(10^10) = 10 ^10 billion, which
is a one followed by ten billion zeros!. Hence we describe e0 as being
equal to w tetration w. But we needn't stop there since we could go to
pentration of w, that is; w tetration w tetration w tetration w tetration
w tetration w. . .etc. . etc. Now if we define 2 sets as having the same
cardinality if there is a one-to-one map between them then we can define
Aleph one as being the first ordinal with cardinality greater than w (which
has cardinality of Aleph zero ---- it is in one-to-one with the Natural
numbers). we can than proceed to Aleph2, Aleph3, Alephw, Aleph(w+)1, Alephw^w,
Aleph(Alephw) and eventually we arrive at a number theta % such that %
=Aleph% and one way of obtaining this is by having an infinite stack of
tetrated Alephs (i.e. a pentration of Aleph) viz. Aleph tetration Aleph
tetration Aleph tetration Aleph tetration . . etc From this we can then
proceed to Aleph%+1,Aleph%+w, Aleph%+1, Aleph%+Aleph w and so on without
end until we arrive at the absolute infinity, Capital OMEGA which is by
definition indescribable and inconceivable
Turing Halting problem
In 1928, Hilbert repeated 3 of his original challenges
of 1900 viz;
1. To prove that all mathematically true statements could
be proved i.e. the completeness of mathematics
2. To prove that only true mathematical statements could
be proven i.e. the consistency of mathematics.
3. To prove the decidability of mathematics, that is the
existence of a decisive procedure to decide the truth of falsehood of
a mathematical statement.
The first two of these were disproved by Godel, while
the third was disproved by Alan Turing (a method which although different,
also relied upon Cantor's diagonal slash technique). Alonzo Church also
disproved the third challenge using a completely different approach. Godel
had shown that there are propositions '&'
(say), such that neither & nor -& is provable , (and as a consequence,
there is no proof of consistency of a formal system 'K'
within that system). Turing on the other hand showed that there is no
general method which tells whether a given formula '$'
is provable within a formal system 'K', or what amounts to the same, whether
the system consisting of K with -$ adjoined
as an extra axiom is consistent
Let Tn(m) represent the result of a Universal Turing
machine that can imitate the nth Turing machine carrying out a computation
on the number m. (e.g. a particular operating system trying to use a computer
program to decide if a particular even number fails Goldbach's conjecture
and cannot be split into the sum of 2 primes). Some of these Tn(m) will
produce a numbered result, while others will run for ever (we will denote
the latter by Tn(m) =& ). Now, assume that there is such a universal
machine H(n,m) that can determine if an answer can be produced.
In other words H 'decides' whether or not the nth Turing machine acting
on the number m eventually stops. For example let the machine output 0
if it does not stop and 1 if it does. Next we use H to eliminate all those
combinations of n and m that do not halt and replace the output with a
0 and then allow Tn to act on m only if H(n,m) =1. Thus our new procedure
is given by Q(n,m) = Tn(m) * H(n,m) and produces a table of infinite dimensions,
which must contain every computable sequence; something along the
lines of
. m--0 . 1 . 2 . 3 . 4. 5 . . . . . .
n
0 . . 1. 3 . 0 . 1 . 8 .
0 . .. .
1. . 0. . 2 . 1 . 3 . 2 .
1. . ....
2. . 4 . 0 . .1. .3 . 0.
. 1 . . . .
3 . .1. . 0. . 2 . 3. 3 .
2 ......
4. . 0. . 0. . 1 . 1 . 7.
0. . . . .
.etc, etc
Finally we apply the slash diagonal technique in which
we add 1 to each diagonal element (i.e. the sequence 1,2,1,3,7 in red,
becomes,3,2,4, 8) to obtain a number which cannot be in the list,
thus demonstrating a contradiction which shows that our original assumption
about the existence of H must have been false. In other words assuming
H exists, there is some Turing machine number, say k, for the algorithm
(diagonal process) 1 +Q(n,m), so we have
. 1 + Tn(n) * H(n,n) = Tk(n)
but if we substitute n = k we get
. 1 + Tk(k) * H(k,k) = Tk(k)
which is a contradiction, since if Tk(k) stops we get
the impossible relation
. 1 + Tk(k) = Tk(k)
since H(k,k) = 1
whereas if Tk(k) does not stop (so H(k,k) = 0 ) we have
another inconsistent result that 1 + 0 = & (i.e. it stops if and only
if, it does not stop!). Hence it is not possible to construct a Universal
machine, that could decide in advance whether there is a number which
contradicts (say) Goldbach's conjecture (which would in effect prove or
disprove such conjectures without actually needing to find such numbers
or proofs!).
Indeed Godel's result follows directly from Turing's (although
historically they were derived the other way round) For Turing showed
that there are some true statements that are not recursively enumerable
and we can can express a Godel statement in this form. So for any formal
system F we can encode a Godel statement G(F), which is
not provable by a Universal Turing machine. So even if F is believed
to yield only true statements, G(F) must escape the net cast by
F despite the fact that we must conclude that G(F) is a
true Turing statement. What Godel and Turing's theorems tell us, is not
that there are unprovable mathematical propositions but rather that whenever
we lay down axiomatical rules of proof beforehand (and if we accept that
those rules are trustworthy), then we are provided with a new means of
access to certain mathematical truths, that those particular rules are
not powerful enough to derive!
......... . . And Yet It Moves"
Galileo was reported to have uttered these words shortly
after he was forced to recant his support for the Copernican' view, of
the sun being at the centre of the solar system. He is regarded as the
grandfather of physics and in actual fact the main reason for Galileo
facing the Spanish inquisition, was due to his book being interpreted
as being rather sarcastic towards the Pope. Indeed it was difficult for
laymen of the time to accept the fact that the Earth actually rotates,
since this seemed to go against everyday experience of spinning objects.
(We had to await Foucault's pendulum for the simplest experimental demonstration
of the Earth's rotation). Much of the story that has passed down is apocryphal
but Galileo was forced to spend the remainder of his old age under household
arrest. Part of his legacy is that of rotational dynamics, and in particular
that of non inertial frames of reference, which produce peculiar effects
and are relevant to both general relativity and quantum theory!
Newton's Laws Of Motion

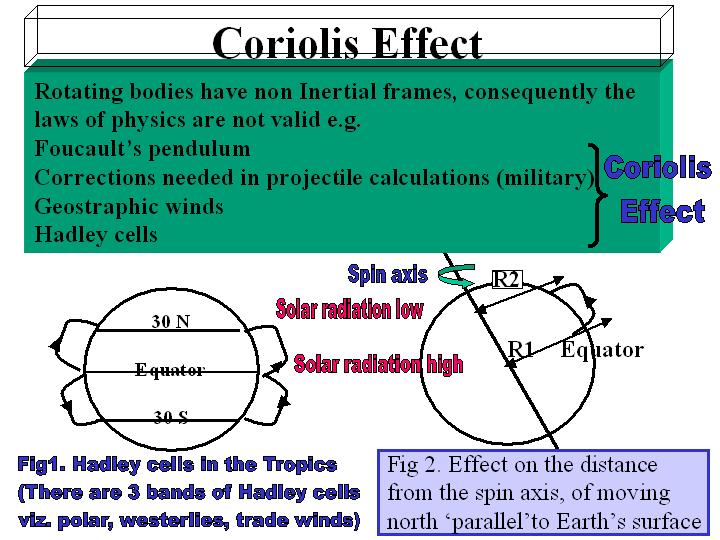
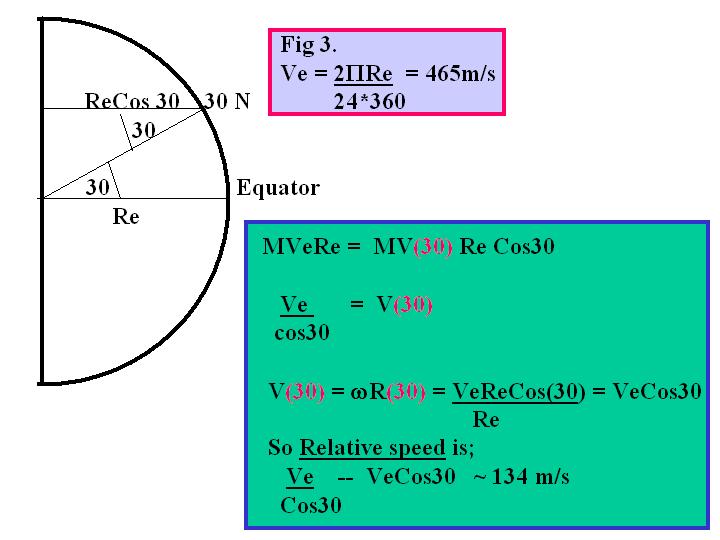
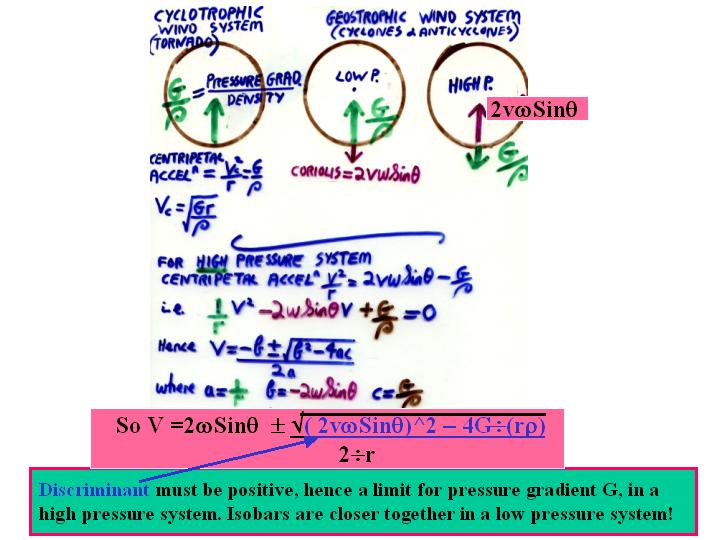
The principles illustrated below have many applications including gyroscopic
compass and gyro-boat stabilizers

g
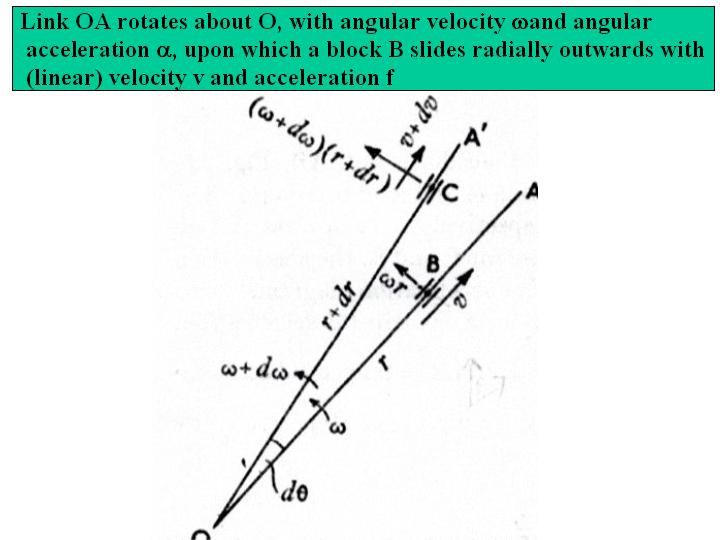
Euler's equations offer a more complete/general description of rotatory
motionl
|