|
|
|

The following articles are contained below:-
Newton’s Second Law and Einstein’s Second Axiom
The Evolution of Einstein's Epistemological Beliefs
Black Hole Information Paradox
"SPACE AND TIME ARE MODES BY WHICH WE THINK RATHER THAN CONDITIONS IN WHICH WE LIVE"
"SUBTLE IS THE LORD ...........MALICIOUS HE IS NOT"
A. Einstein
When Einstein was a boy he imagined what it would be like to ride along a beam of light. He was aware that Maxwell’s equations described light as being a fluctuating electromagnetic field but to such an observer, Maxwell’s wave would appear stationary and therefore not self sustainable. Hence Einstein’s thought experiment or Gedanken, to use the correct German term, highlighted an inconsistency. A sinusoidal electric field generates a similarly oscillating magnetic field, which in turn generates the original oscillating electric field, but to an observer who travels at the speed of light, no such temporal variations are observed and hence the electromagnetic field cannot be self-propagating. Another form of this gedanken is where Einstein imagined looking at himself in a mirror whilst travelling at the speed of light. Light was believed to travel through the luminiferous ether, which pervades all manner of mediums, including a vacuum and could therefore be assumed to have a fixed (e.g. zero) velocity relative to absolute space. If an observer travels through this medium at the speed of light, the rays from his body would never reach the mirror and hence he would be unable to see his reflection. [The speed of light squared is numerically equal to the reciprocal of the product of the permeability and permittivity of free space.] Hence it would be possible to single out a particular inertial reference frame, as all others would be able to see their reflection. Such a detectable absolute reference frame would consequently undermine the Galilean belief that all inertial frames are equivalent and that no physical observation could distinguish between any two. [An analogous reflection of sound waves is not a problem since the medium e.g. air, is dragged along with the observer’s laboratory.]
It took Einstein a further 10 years before he was able to resolve this conflict that he had brought to light with his gedanken. His Special theory of relativity showed that the speed of light is constant for all observers (c.f. ** below) and this is enshrined as a physical law. The relative nature of constant (inertial) motion is retained but only at the expense of insisting upon the relative nature of space and time. In particular, these had to be fused together in a pseudo-Euclidean manifold i.e. all physical laws had to be written in the framework of a 4 dimensional space-time continuum.
His gedanken did not stop there however. He was aware of the problem of upholding Special relativity when considering gravitational fields. Light was believed to move in a curved parabolic path when falling in a (locally uniform) gravitational field, as did all entities. The lower edge of a ‘vertically wide’ curved beam would not be as long as the top edge and this would imply that the speed of light would be slower there, which would conflict with the second axiom (the constancy of the speed of light). Einstein’s solution was to claim that the time of travel along the lower edge was less than that of the upper and that this time dilation was actually responsible for what we experience as a (Newtonian) gravitational influence.
Another problem was how to generalize Special Relativity so as to incorporate
motion that was non-inertial (e.g. a linearly accelerating system), since at
any instant, such an object would have a particular velocity that would produce
an observed contraction in length and dilation in time. However non-inertial
frames were regarded as being absolute rather than relative and if the object
was a rapidly rotating disc, in which the rim was traveling close to the speed
of light, the circumference would contract enormously, unlike the diameter.
The ratio of the two would consequently be far less than the usual value of
pi, in other words, space becomes warped! [The difference between general and
special relativity is that in the general theory all frames of reference including
spinning and accelerating frames are treated on an equal footing. In special
relativity accelerating frames are different from inertial frames. Velocities
are relative but acceleration is treated as absolute. In general relativity
all motion is relative. To accommodate this change general relativity has to
use curved space-time. In special relativity space-time is always flat. The
only sense in which special relativity is an approximation when there are accelerating
bodies is that gravitational effects such as generation of gravitational waves
are being ignored. But of course there are larger gravitational effects being
neglected even when massive bodies are not accelerating and they are small for
many applications so this is not strictly relevant. Special
relativity gives a completely self-consistent description of the mechanics of
accelerating bodies neglecting gravitation, just as
Newtonian mechanics did.]
It was considerations such as these that eventually led Einstein to his greatest gedanken and produced the principle of equivalence. He was very impressed with the observation that inertial mass and gravitational mass had been measured to be the same, to a very high degree of accuracy. He therefore claimed that a linearly accelerating body would observe all inertial objects, to be ‘falling’ in the opposite direction, as if they were in a (localized) gravitational field. An astronaut accelerating in deep space, far from any gravitational mass, could easily be convinced into believing that a nearby planet was causing the reaction between his feet and the floor of the spacecraft, giving the sensation of weight. [Likewise we all experience a perceived increase in our weight in a lift, when it is initially accelerating upwards.] Hence gedankens have now led to the following conclusions.
Unlike a constant accelerating frame of reference, the strength of a gravitational field around a spherical mass varies with the distance from its centre. Hence Einstein needed a radical way of mathematically expressing how a gravitational field would warp his 4 dimensional space-time of special relativity. After much searching he realize that the so-called contracted Bianchi identities that are associated with Riemman geometry, offered the ideal solution and the Newtonian concept of a gravitational mass, was replaced by that of a curved space-time, which determined how a test particle would move. Such tensor calculus allowed a generalisation of special relativity to that of non-inertial (accelerating) frames and offered a revolutionary insight into the nature of gravity.
In later years Einstein would again resort to gedanken in order to try to show-up any shortcomings in Quantum theory. He often played the devil’s advocate but Niels Bohr managed to find a lacuna in each of Einstein’s attempts and was able to demonstrated the consistency of his Copenhagen interpretation, {c.f. the aside below}. Einstein, although not succeeded in undermining quantum theory did in actual fact put it on a more definite foundation as a result of his gedanken. In recent years the Einstein-Podolsky-Rosen argument (which attempted to support the hidden variable approach to quantum theory), has been utilized in Bell’s inequality and this has been tested by Aspect et al. The conclusion of these results vindicates Bohr’s stance and demonstrates that even if quantum theory is superseded, we still have to contend with the experimental result of a non-local reality!
ASIDE
Ironically Bohr used general relativity to shoot down some of Einstein’s own objections to Heisenberg’s Uncertainty Principle, by utilising the fact that time is dilated in a gravitational field. Indeed gedanken using quantum theory can be used to deduce the first order magnitude of such time dilations. Consider a photon of frequency f1 = 1/T1 rising a distance H in a gravitational field of local value g, whereupon it experiences a gravitational red shift corresponding to a new frequency F2 = 1/T2
E1 – E2 = mgH
hf1 – hf2 = mgH . . . . [Since E=hf, also f =1/T]
h/T1 – h/T2 = mgH
h?T/(T1*T2) = mgH where ?T = T2 - T1
If ?T is small then T1 ~ T2 =T(say) . . therefore
h?T/T² = mgH = (E/c²)gH . . . . since E = mc²
h?T/T² = (h/Tc²)gH
?T/T = gH/c² and therefore g =?Tc²/(TH)
An alternative drivation can be obtained by considering a beam of light moving (in a parabolic arc) under the influence of a gravitational field. While the top of the beam moves a distance cT the bottom of the beam moves through a distance c(T-t), hence the difference in upper and lower paths is ct. Also the downward component of the beams velocity must be the same as the downward speed of any falling mass namely gT. By using similar right angle triangles we obtain the following ratio;
ct/gT =h/c
and so as before,
t/T =gh/c^2
Hence time moves more slowly in a gravitational field (about o.ooooooooooooo1% less between ones head and feet) but this tiny difference is not only sufficient to bend light, it is sufficient to cause (Newtonian) gravity. [Interestingly it can be shown from classical electromagnetism that the energy of light is equal to its momentum multiplied by c, in other words, even using 19th century physics, we can infer the mass energy equivalence E=mc^2 . This in turn means that an objects mass must increase with its kinetic energy and hence with its velocity which also implies - via Newton's second law - that time dilates and space contracts for a moving observer!. Also by starting from the time dilation result derived from the curved (parabolic) beam of light, we are able to reverse the steps taken above and deduce that the energy of light is proportional to its frequency, which pre-empts the results of quantum theory!]
However the above arguments relating to time dilation, do not account for the corresponding warping of space. Consider one last gedanken, in which a bullet is fired in deep space between two fixed points. If the experiment were to be repeated but this time with the bullet having to pass through a whole drilled through the diameter of the planet, it would take less time to complete the same journey, as could be determined using Newtonian gravity. However if the whole experiment were to be done using a light pulse instead of a bullet, the light would actually take longer the second time, when having to pass through the central core of the planet! This is because gravity actually warps space and this effect cannot be accounted for using Newtonian gravity. Such subtle differences only become significantly noticeable when one deals with extreme speeds (~ c) or large gravitational fields but the two theories are non the less fundamentally different.

Special Relativity is based upon operational definitions and is logically self-consistent once we accept the two axioms on which it is founded ( invariance of the laws of physics in inertial frames and the constancy of the speed of light**). Einstein derived his theory from considerations of Maxwell’s laws of electromagnetism, which were the first equations to be Lorentz covariant as opposed to obeying Galilean transformations. Hence there cannot be an inconsistency between the electrodynamic situation that Don refers to and Special Relativity. [Indeed his article provides a good illustration of the conflict between electromagnetism and Newtonian mechanics.]
A magnetic field can be considered as being our sense perception of movement relative to an electric charge. Electric and magnetic fields transform into each other (Maxwell’s equations) as our relative motion alters, in tune with the transformation that occur between space and time (Lorentz’ equations).
To avoid mathematical detail (*!), I will simply say that the purely electric field experienced by observer "A" moving with the spherically expanding charges, is perceived as a flattened sphere by observer "B" to whom the system is moving. Although B experiences an additional magnetic field, which would tend to cause the electron to become squeezed into a rod, this is exactly ‘compensated’ for by the changes in the space and time co-ordinate system of B.
It may also be of worth to note the following two points. Firstly in Relativity, ’seeing’ is different from ‘observing’ e.g. a book lying on its side, would not only contract with velocity but also appear as if its forward face is rotated away from the observer. This is an additional effect due to light from the far edge taking longer to arrive than that from the near edge. However for a sphere R. Penrose has proved that the two effect cancel out so that although the sphere is observed as being flat what we see is a perfect sphere, due to this rotation effect.
Secondly, consider the flattened sphere of charge passing observer B and assume that in his reference frame, it has expanded so that the front and back edge just fit within his body at the same time. According to A the charge distribution is spherical and the diameter at that instant is greater than the width of observer B! This is just an example of the ladder in the barn paradox and as with the twin paradox, it only arises when one fails to apply Relativity theory consistently. The flaw in the above case arises because we fail to realize that the first casualty in relativity theory is simultaneity.
The Special theory of Relativity explains the way electric and magnetic fields transform into one another as the motion of an observer alters and reveals the nature of electromagnetic waves. However General Relativity extends this so as to cope with accelerating frames and gives us a description of gravity. In particular it shows that as an observers speed increases, there is no such transformation as that which occurs with electromagnetic fields but instead the field tensors alters in a way that is consistent with there being a relativistic increase in the gravitational mass of the source. This shows the inherent difference between the two fields and in particular light and gravitational waves, even though they are consistent with each other via special relativity.[This difference is further highlighted in quantum field theory, where gauge fields that are purely attractive (e.g. gravity) have to be mediated by an even integer boson (a graviton has a spin of 2h) while the photon is a spin 1h boson.].
As a footnote:
*! In all cases the interaction between charged particles is independent of the frame of reference used, although the division between magnetic and electric forces depends upon the frame. The behaviour of these charged particles is given by the relativistic form of Lorentz’s equation viz;-
Q(E = V*B) = d/dt{mv/sqroot(1-v^2/c^2)}
The magnitude of E, v and B will each depend on the reference frame in which they are being measured. The interchange between electric and magnetic forces when the reference frame is changed is a case where even small velocities bring in relativistic change in the description of forces, (but relativistic changes in the dynamics of a moving charge become important only at velocities approaching the speed of light.)
**Einstein's theory states that in an inertial frame, nothing can exceed the speed of light (note that the speed of light is rarely constant in non-inertial frames) , however a more recent formulation known as DSR (Double Special Relativity) suggests that the speed of light itself varies according to the energy scale being considered and hence the wavelength ('colour') of light. This theory has been invoked in order to overcome certain problems in quantum gravity ( viz. the Planck cut-off energy for photons is, due to Doppler shift, dependent on the directional and speed of the observer and would not therefore be invariant,) as well as explaining the observed preponderance of extremely high energy cosmic rays.
Such ideas would also fit in with theories involving a variable cosmological constant, that are used to explain the recently observed acceleration in the expansion of the universe, as well as solve the horizon, flatness and missing mass problems (c.f. Quantum Theory). Einstein's equation shows that if the vacuum has a positive energy density (which equals lambda multiplied by the forth power of the speed of light), it will posses strange properties, such as a negative pressure (which will dominate), causing a repulsive force between points in space! In one such formulation involving a variable speed of light (c) at the birth of the universe, "c" decreases sharply and lambda is converted into matter as the Big Bang occurs.[ This formulation involves terms of the form (dc/dt)/c ] As soon as lambda becomes nondominent, the speed of light stabilizes and the universe expands as usual. However a small residual lambda remains in the background, and eventually resurfaces as an accelerated expansion (like inflation) as has recently been claimed to be observed using the results from studying supernova in distant galaxy clusters. But as lambda proceeds to dominate the universe in which matter has pushed away to produce mainly empty space, it again creates conditions for another sharp decrease in the speed of light "c"and a new Big Bang and a fractal universe is envisaged!
Evidence for a varying "c" has been suggested from examining the fine structure constant alpha associated with the spectra of distant and hence erstwhile nebula, and also by the observation of cosmic rays that are beyond the freshold limit of energy predicted by the theory of meson creations. Such high energy protons should collide with cosmic radiation photons producing mesons and in doing so no longer exist with such high energies as observed - unless the speed of light is greater for such high energy processes.
Einstein's field equation relates space-time curvature to energy density and this proportionality constant contains the speed of light. Hence varying "c" requires a violation of energy conservation and it transpires that if the universe is positively curved (i.e closed) then energy evaporates from the universe but if it is negatively curved then energy is created out of the vacuum in such an open universe. [Also note that conservation of energy imply that the laws of physics must remain the same through time - including the constancy of light - hence altering "c" implies a violation of energy conservation] This has dramatic consequences in that it ensures that the mass in the universe stays close to the critical density of a flat universe as observed! Also if the speed of light is reduced the (positive) vacuum energy is also reduced (as does its negative pressure and hence its repulsive force) and this explains why the universe is not dominated by the cosmological constant lambda which would otherwise be the case as the universe expanded.[The matter density obviously reduces with time but under inflationary models any remnant of lambda, would remain constant and would therefore have an ever increasing dominance] This effect also reinforces the observed homogeneity since overdense regions would lose energy while underdense would gain energy from the vacuum. In summary a varying speed of light solves many cosmological problems viz. those relating to flatness (& lambda), horizon, monopoles, homogeneity, and the non dominance of the cosmological constant.
The early universe therefore consists of just lambda but if it is coupled to the speed of light, its initial high value is unstable against fluctuations and it rapidly decreases. This has two effects, firstly the value of c decreases and secondly matter is created at the expense of lambda. A possible mechanism for this may involve the expansive nature of lambda and the consequential decrease of c with the corresponding reduced energy scale (as in DSR above); since lambda is expansive any virtual particle pair production (allowed by Heisenburg's UP) could become permanent! The lowered value of c means that the energy deficit is reduced and could be offset by say the negative gravitational energy created as the pair separate. [Since lambda depends on the zero point energy of the vacuum, a reduction in c could alter the energy contributions of the bosons (positive) and fermions (negative) as dictated by supersymmetry]. This would be consistent with Einstein's field equation, since the reduction in lambda would require an increase in the matter/energy density in order to maintain a flat universe, all of which can be catered for by a reduction in c. In other words the curvature tensor corresponds to a flat universe and is maintained that way as the universe expands, as a result of the decreasing c, which links curvature to the energy density via Einstein's equation.
Even without a varying speed of light, if the universe does have a non zero cosmological constant, it implies that the missing mass is not as great as it would otherwise be. The flatness of the universe depends on 3 factors; the amount of visible mass and energy, the value of lambda, and the amount of dark matter. Some of this dark matter is known to exist, from the study of galaxy rotations and galaxy cluster dynamics, however it is not known for sure as to the nature of this invisible source. Suggested candidates include WHIMPS (weakly interacting massive particles) MACHOS (massive compact objects) or a small but significant mass being associated with the abundant neutrino (as indicated by the observation that neutrinos can change flavour).It is not however known if this dark matter is enough to actually produce a flat universe since as already stated this depends on the value of lambda (the larger the cosmological constant is, the smaller the missing mass contribution). The most favorite candidate for the missing mass is however the axion which is predicted by the QCD. Without invoking an axial field with mass, strong interactions would indicate a violation of CP (charge - parity) which is not observed (for example the neutron electric dipole is known to be very small).
Some string theories permit the spontaneous breaking of Lorentz symmetry in the early Universe, which would result it being filled with a background fields that had a preferred (spontaneously chosen) direction. These background fields would violate particle Lorentz symmetry (i.e. an elementary particle moving in the presence of one of these fields would undergo interactions that would have a preferred direction in space-time), but maintain observer Lorentz symmetry. Although these effects would occur at the Planck scale (~!0^19Gev), it may be possible to make measurements on a lower scale (say that of a proton ~1Gev), providing we compensate with a high enough degree of accuracy (e.g. if we do experiments on protons that are sensitive to one part in 10^19). We would then, in effect, be probing the Planck scale and be able to confirm or eliminate such conjectures.
The entropy of a black hole is proportional to the area of its event horizon and has an enormous value. [Entropy can be regarded as a measure of how probability that system is to come about by chance] Now because of the large black holes at the centres of galaxies, this black hole entropy easily represents the major contribution to the entropy of the known universe! Because of the second law of thermodynamics, the entropy at the beginning of the universe must be very small, this beginning is represented by the singularity of the big bang, which must be extraordinarily special or fine tuned compared to the high entropy singularities that lie at the centre of black holes. It therefore requires a new theory -- quantum gravity -- to explain the remarkable time asymmetry between the singularities in black holes and that at the big bang.
Newton’s Second Law and Einstein’s Second Axiom
There is an appealing way to derive E=Mc^2 from Newton’s Second Law and Einstein’s Second Axiom as follows:-
Force = rate of change of momentum i.e.
F = Mdv/dt +vdM/dt
If mass is constant and velocity changes then,
dE=fdx
and dx=vdt
therefore dE=M(dv/dt)*(vdt) =Mvdv
Integrating, E=mv^2
However, if the velocity does not increase (as with light) but the mass changes,
F=v(dM/dt)
dE = v(dM/dt)*dx = v(dM/dt)*vdt
If v = c, dE = c^2dM
Integrating, E = Mc^2
Alternative proof;
Consider 2 colliding photons of equal energy (and mass M), undergoing Compton scattering and each recoiling in opposite directions with the same original magnitude of momentum (i.e. Mc) as viewed by a defined "stationary" observer. When viewed by an observer moving to the left with velocity v relative to the original frame of reference, the right recoiling photon will have an increased momentum of say (Mc + mc,) compared to that of the left recoiling photon of momentum (say) Mc. Hence the total momentum of the system of the two photons will be just (Mc+mc) -Mc = mc. If we consider the original frame, with the photons momentarily at rest at the instant of collision (e.g. as with a particle/ antiparticle pair production with no residual momentum), then as viewed by the new frame, the momentum of the system will then be (M+M+m)v .
In other words we have the following relationship
(M+M+m)v =mc
Now the energy that is added to the right recoiling photon equals the force it experiences multiplied by the distance moved or;
E = force* velocity* time
but force*time = change in momentum = (Mc+mc)- (Mc) =Mc+Mc+mc
therefore E = (Mc+Mc+mc)v =c(M+M+m)v =c*mc =mc^2
* * * * * * * * * * * *
Also note that prior to Einstein's theory, it was known from Maxwell's theory of electromagnetism (EM), that the energy of such EM radiation was equal to its momentum multiplied by c. This therefore sugested the relationship (at least for EM radiation) that E =mc^2, where mis the mass of a photon. Now if we accept this relation as being fundamental to physics, then we can recover the formula for the relativistic increase in mass for a moving body (and hence the accompanying time dilation and length contraction) in the following way;
Power = dE/dt = Fv
i.e . .d(mc^2)/dt = d(mv)/dt*v
multiply both sides by 2m
. . . . . 2mdm/dt*c^2 = 2mmdv/dt*v
integrating wrt dt gives
2mdm*c^2 = 2mmdv*v
then integrating both sides wrt their integrand gives,
[c^2m^2]limits(m, mo) = [v^2m^2]limits(v,0)
c^2m^2 - c^2mo^2 = v^2m^2
c^2m^2 -v^2m^2 = c^2mo^2
m^2(c^2 - v^2) = mo^2c^2
c^2mo^2 = m^2(c^2 - v^2)
mo^2 = m^2(c^2 - v^2)/c^2
m = mo/SqRt[1 - (v/c)^2] = mo*gamma . . . . . . as required
The Evolution Of Einstein’s
Epistemological Beliefs
By the turn of the century
events had prompted Lord Kelvin to remark
The
avant-garde Einstein however, although sensing the spuriousness
The latter half of the
19th century had witnessed a considerable move
"If I pursued a beam
of light with velocity c I should observe such a beam as a spatially oscillating
electromagnetic field at rest.
The need for operational definitions and their primacy to
Almost as if to
complete the destruction of the ether he published, that
Mach's
positivistic convictions also refuted the existence of atoms
The
second conflict that had arisen between Newtonian mechanics (as applied to atoms)
and the concept of electromagnetism (as applied to the
Having eradicated
the concept of simultaneity from his special
Indeed 'Mach's Principle' itself entails some instantaneous
This realism
was to be of major importance during the 5th & 6th
By fusing space
and time Einstein had achieved a unity comparable with that of Maxwell.
The aesthetic appeal of a symmetrical field, his desire for greater unification
and the establishment of an objective microscopic
This
quest for the Holy Grail eventually placed him in an
Analogous to the dualist's
description of the mind as being the ghost
The
visionary had become a critic. Although acknowledging the e
Einstein's Theory Of Relativity
At the beginning of the last century it was believed that most of physics was
well understood, there were just two seemingly small dark clouds, which obscured
our otherwise impressive view of the physical world. These two problems related
to the inability to detect the luminiferous ether and the statistical anomaly
in black body radiation. These 'small' clouds on the horizon did however grow
to gigantic proportion, casting a gloomy shadow over the physics community,
which resulted in two great revolutions viz. Relativity and Quantum theory.
The conflict between Newton's particle mechanics (as exemplified by the success
of statistical thermodynamics) and Wave theory (as exemplified by Maxwell's
laws of electromagnetism ) becomes evident when we study Black body radiation
and its resolution resulted in the downfall of classical physics and birth of
Quantum Theory! Another such conflict is 'brought to light' when we consider
the propagation of electromagnetic radiation (light) and the Newtonian view
of space and time, one that can only be resolved with Special Relativity.[Fig
#1]. In his theory Einstein demolished the concept of the luminiferous Ether
(the medium through which light waves were thought to propagate) and this article
is a brief summary of the events and reasoning, which lead to this revolutionary
theory.
According to Galilean relativity, the laws of physics are the same for all inertial
frames. [These are defined by Newton's first law of motion and correspond to
observers that are moving at a constant velocity i.e not experiencing any acceleration].
With the advent of Special Relativity, the laws of physics were no longer valid
under Galilean transformations but instead had to be Lorentz covariant and Maxwell's
equations of electromagnetism were unintentionally the first to be written in
this form. The inability to detect the Ether was an indication that our understanding
of space and time was flawed and eventually culminated in Einstein's general
theory of relativity, which not only discarded the notion of an absolute space
and universal time but also demonstrated that gravity was a manifestation of
a curvature in the space-time continuum. Matter tells space and time how to
warp and these in turn determine how test particles move (along geodesics of
maximised space-time intervals, or proper time). Newton's laws are Galilean
covariant whereas Maxwell's laws are Lorentz covariant. Maxwell's equations
lead directly to a wave equation of electromagnetism and hence the speed of
light itself, is naturally a relativistic law of physics. Both Galilean and
Lorentz transformations relate to inertial frames moving at constant velocity
but the latter arises due to the 'constancy of the speed of light', being elevated
to the status of an actual law of physics, something which was unknown to Galileo
et al.
Einstein later developed his theory so as to be applicable even to non inertial frames (those that are undergoing acceleration). By making acceleration relative, Einstein completely undermined Newton's belief in an absolute space, since in Newtonian mechanics the laws of physics are only valid in inertial frames and acceleration is not relative but absolute (which infers the notion of an absolute space). Here we will be concentrating on the special theory of relativity and will only briefly allude to the general theory, which will be dealt with more thoroughly in a future article.
Einstein's Special Relativity (SR) resulted from his study of Maxwell's Laws of Electromagnetism (EM), while the need to extend this theory for non uniform motion (acceleration) and also to make it valid in gravitational fields, led to General Relativity {GR}. [We can therefore considered SR as being a limited case of GR]. Special Relativity explains the constancy of the speed of light in empty space far away from any matter, while GR explains the local constancy in a gravitational field. SR is mandatory when dealing with very high velocities comparable to the speed of light, while the incredible accuracy GR becomes evident when dealing with (large) gravitational fields. Let us now look again at the reasons why Einstein was driven to redefine our understanding of space and time.
As a boy Einstein imagined riding along a beam of light at the same speed 'c', whose waveform would therefore appear stationary. According to Maxwell's theory there is no such thing, since he had shown that light is an oscillating electromagnetic field. The young Einstein imagined what he would see if he looked in a mirror which was travelling with him at the speed of light. Would he see his own reflection, or would he see nothing due to the fact that light from his face would never be able to catch up with the mirror and not therefore be reflected to his eyes. According to Newtonian physics, the light from his face would never reach the mirror if he travelled at the speed of light and he would no longer be able to see himself. Hence he would be able to say that he was travelling (in an absolute sense) at the speed of light, in contradiction to the principle of (Einsteinian & Galilean) relativity. So we need to recognise that the speed of light is the same (300 000 000 m/s) for all inertial frames, irrespective of their velocity. Einstein was the first to realise that the concept of an Ether was a myth, but that instead we needed to redefine the nature of space and time.
This was Einstein's earliest realisation that the speed of light must be constant for all observers and the need to elevate this fact to a physical law (which is more rigorously demonstrated by Maxwell's equations), resulted in the relative nature of space, time and mass. Consider an observer moving at half the speed of light (relative to us). If he is approaching us and we shine a beam of light towards him, Newton & Galileo would say that it must pass him at one and a half times the speed of light, whereas if he were moving in the same direction as the beam, it would overtake him at just half the speed of light. However according to Maxwell's laws of electromagnetism, the speed of light must be the same for all observers; so who is correct? Originally, most people would claim that Newton's mechanics were correct but Einstein realised that it was Maxwell's laws, which were valid (they were the first ever laws of physics to be Lorentz covariant - - - - space and time are relative)
Einstein was influenced by Immanuel Kant's view, that space and time were products of our perception. In other words, what we know of the world conforms to certain a priori categories, which although we recognise by experience do not arise from experience. These categories (e.g. space and time) are laid down by the mind and turn sense data into objects of knowledge. "Space and time are modes by which we think rather than conditions in which we live" [EINSTEIN]
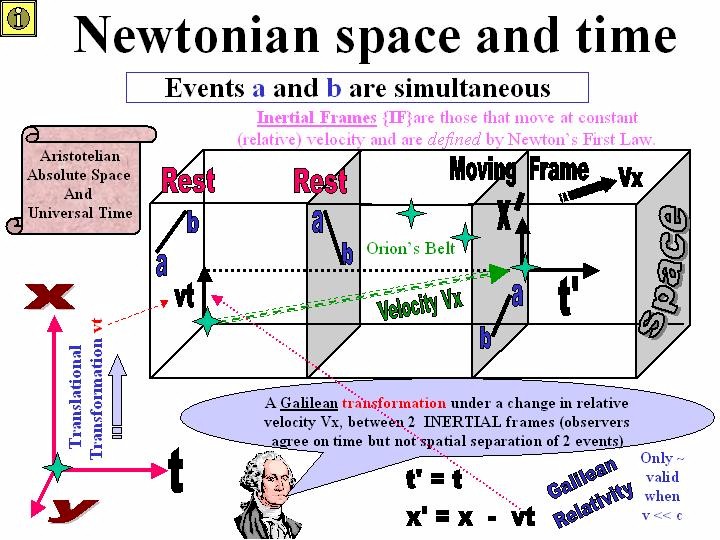
FIGURE 1
Newtonian physics has an absolute 3 dimensional space and a separate universal time. All observers 'slice' their world into the same sections of space and time. The pairs of events marked 'a' and 'b' in each space frame, represent events that are simultaneous to all observers, such as 2 people striking a match at the same time (although their spatial position and separation could change with time, as depicted in Figure 1). Here we have a Galilean Relativity, in which the known laws of physics are the same for all inertial frames (and all constant velocity motion is relative). However, although observers moving at different relative speeds share the same time, they have different distances. Galilean transformations do not however accommodate the laws of electromagnetism and this is an indication of the inadequacy of this erstwhile understanding of space and time. As we shall see, the laws of physics become of primary importance in Einstein's theories and it these laws which indicate the nature of our personal space time, rather than the other way around. In some respect we may say that our personal space-time must transform in such a way, so as to tolerate these physical laws [This is particularly so in the final form of Einstein's theory - General Relativity]
Galileo
had replaced Aristotle's view of a single absolute space through which objects
moved over a period of time, with the notion of separate inertial frames connected
by time. In this view all 'smooth, uniform motion' is relative and the laws
of physics are the same for all such inertial frames. Einstein elaborated Galileo's
notion of relativity so as to include Maxwell's laws of electromagnetism (SR)
and later extended this symmetry principle (relativity) even further, so as
to include non inertial frames (GR).
Note that in Figure #2, what actually occurs are not mere 'rotations' of the
axes (which would be valid if all 3 axes were spatial), but rather more sophisticated
Lorentz transformations, acting upon a pseudo-Euclidean manifold. {Both 'x'
and 't' coordinates are actually 'rotated' in towards each other, as depicted
in the axes in the lower left hand corner.) The term 'COVARIANT' refers to the
fact that the laws of physics looks the same all coordinate systems. Covariance
means that both sides of an equation change in the same way, preserving the
validity of the equation (whereas invariance means that nothing changes) The
need for operational definitions and their primacy to perception, are very much
in accord with the critical positivism of Mach, who had strongly influenced
the young Einstein. Let us go back to basics and put relativity on a firm foundation.

FIGURE 2
As artists know, the apparent shape and apparent dimensions of objects can change when viewed from different angles. However there are invariants, even though the actual projections along our length, width and height (x, y and z axes), are different in each case. For example, the distance between the diagonal corners of a 3 dimensional box is invariant, as indeed is its volume, so we would say that these properties are symmetrical under a rotational transformation. Now symmetry under translation leads to conservation of momentum and energy, while symmetry under rotation explains the conservation of angular momentum. Symmetry also allows unification of the fundamental interactions. Einstein was the first to realise that other transformations can also take place when an observer undergoes a boost in their velocity. He was therefore keen to establish what these changes are and what were the invariants (in 4D space-time but not space or time alone). Hence Einstein preferred the name 'Invariance Theory' rather than the 'Relativity Theory'. Special Relativity expressed/restored symmetry under boosts in velocity (inertial frames), while his General Relativity (GR) went on to make the laws of physics covariant (symmetrical), under acceleration (non inertial frames) and produced a new understanding of gravity.
Maxwell's
laws predict a constant speed of light 'c', even for observers moving rapidly
towards or away from light source (confirmed by Michelson & Morley and other
experiments). This requires relative space and time! Maxwell's laws were the
very first to be Lorentz covariant and thus demonstrate the fallibility of the
Galilean transformation. but the Lorentz transformation does reduce approximately
to the Galilean transformation when the speeds involved are small compared to
the speed of light. The Lorentz 'gamma factor' is so close to unity for most
terrestrial speeds, that SR effects are not noticeable in everyday experience
The Lorentz transformation only become noticeable at speeds close to that of
light, whereupon the gamma factor is significantly greater than unity and is
a measure of how much length contracts and time dilates for a moving frame
The significant differences between the transformations of SR compared to Galilean
relativity, is that it is not restricted to simply rotations and translations
and reflections but also boost transformations due to a change in relative velocities.
All these together constitute what is referred to as the so called Poincare
transformations, in which it is not just the 3 spatial axes that are transformed
amongst themselves but also a space axis (in the direction of motion), is transformed
(mixed) with the time axis.
Hence
different moving observers slice up their space and time differently as depicted
in Figure #2 above. The result of this is that clocks will appear to be out
of phase with each other along the length of a moving object. This means that
if one observer (the blue axes in Figure #2), sets up a line of clocks that
are all synchronised so they all read the same time (e.g. events 'a' and 'b'),
then another observer who is moving along the line at high speed (the red axes),
will see the clocks all reading different times. Observers who are moving relative
to each other observe different events as being simultaneous - - - - each observer
will have their own plane of simultaneity.
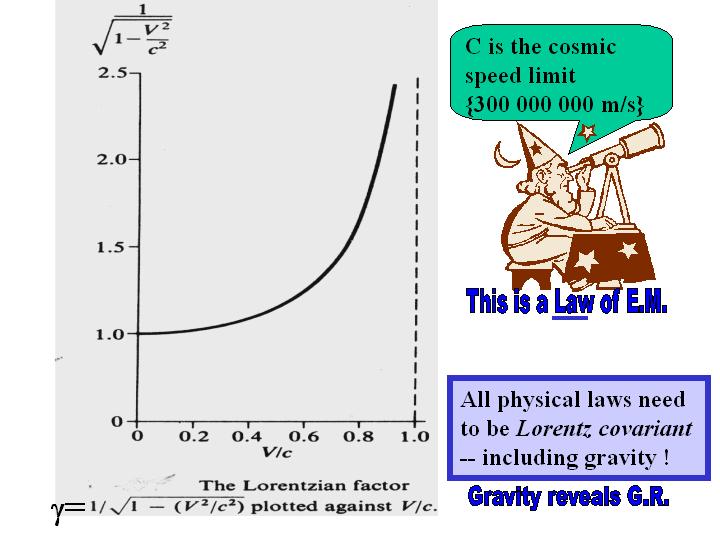
FIG 3
Einstein
regards space-time as a four-dimensional continuum in which observers travelling
at different speeds slice their space and time into different 'foliations'.
The net effect of this four-dimensional universe is that observers who are in
motion relative to you, seem to have time coordinates that lean over in the
direction of motion, and consider things to be simultaneous that are not simultaneous
for you. Also spatial lengths in the direction of travel are shortened, because
they tip upwards and downwards, relative to the time axis in the direction of
travel, akin to a rotation out of three-dimensional space
So the events marked (in blue), 'a' and 'b' are simultaneous in the 'moving'
(blue) frame but 'a' clearly occurs before 'b' in the 'Rest' (red) frame. As
an analogy, consider the statement "the chimney of the house across the
road is directly behind a telegraph pole". This may be true for me but
not for a person standing a few feet away. Likewise in SR we have to accept
the fact that people have significantly different 'realities' depending on their
relative speed. So the bare statement that "these two events occurred at
the same time", is meaningless unless one adds "according to this
observer". [We will examine this loss of simultaneity in Figure #4 below.]
This loss of simultaneity is relevant to GPS systems since the notion of 2 signals
sent simultaneously from 2 different orbiting satellites, is not simultaneous
for the stationary observer receiving it on the ground and vice versa and this
has to be corrected for, when estimating the global position of an observer.
Hence observers will not agree upon the time interval between event a and b
(which are actually regarded as simultaneous in the blue frame). Also note that
SR states that there will be a time dilation effect to take into account because
of the speed of the satellite, while GR states that there will be a counteracting
speeding up of time due to the weaker gravitational field, which is of a greater
magnitude than the SR effect.
Relativity
tends to view space-time as single 'frozen ice block' (containing both past
present and future), in which individual observers are able to illuminate different
slices according to the tenets of SR. This is in contrast to 'the river of time'
and views which relate to the flow of time's arrow. "For we convinced physicists,
the distinction between past present and future is only an illusion however
persistent"[EINSTEIN]
Einstein's theories do however emphasise a perennial philosophical problem,
in that his block view of space-time does not differentiate time into a past,
present and future. In other words there is no 'NOW' to distinguish past from
future or give a special significance to being in the present (this is known
as the problem of transience).
Now consider the Blue Inertial Frame. Suppose events 'a' and 'b' corresponds
to the front and back of red's ruler, coinciding SIMULTANEOUSLY, with the front
and back of blue's ruler (top left hand diagram). This defines the length of
red's ruler in blue's frame. However according to the Red Frame, when the back
of his ruler is in line with the back of blue's ruler (event a), the front of
blue's ruler has not yet aligned with the front of his ruler (event b is in
the future of event b). In other words red regards blue's ruler, as being shorter
than his (ac in top right hand diagram). Hence loss of simultaneity leads to
different measurements of the length and time interval between events a and
b but spacetime 'interval ab ' is invariant.
Just as different people around the world have different perspectives on the time of day, orientation of the stars, different languages, alphabet and even numerals, we now need to appreciate that different observers may also have their own personal perspective on space and time; this is even more evident when we study General Relativity. As in life, where an individual is determined by the sum total of their experiences, in the physical universe, space-time is composed of 4dimensional events and two events may be simultaneous to one observer but not to another moving inertial frame Henceforth space and time will be treated as a 4dimensional manifold, rather than an absolute 3 dimensional space with a distinct time, which flows universally. "Common sense are those layers of prejudice that are laid down before the age of eighteen" [EINSTEIN]
The
human mind likes to slice up the 4D continuum into 3D of space and 1D of time
(a computer for example, might be quite happy to think in terms of a 4D space-time).
This is analogous to deciding to cut up a batch loaf of bread, into parallel
slices. However Einstein was the first to realise that observers moving at different
speeds, slice up their space in different orientations. The 2 axioms of SR are
shown in Figure #4 where it is demonstrated that elevating the constancy of
the speed of light to an actual law of physics, brings about a downfall of simultaneity
and this in turn implies the relative nature of space and time
FIGURE 4
As observed by all 3 spaceships (who are at rest in deep space relative to each other), the light signals from the middle ship, arrives at the outer 2 ships at the same time (due to the second axiom above). This conflicts with the 'moving' observer, whose worldview is depicted above. \Because he sees the 3 spacecrafts moving together with a velocity 'V', he observes the light arriving at the rear spaceship first! Einstein realised that time must move at different rates for different observers, if light moves at the same rate for all observers.
An
equivalent explanation is as follows. Consider a man at the centre of a moving
railway carriage who strikes a match. From his point of view, the light from
the match hits the front and back of the carriage simultaneously. However from
the viewpoint of a man standing on the platform (who is aligned with the man
when he strikes the match), the light from the match reaches the back of the
carriage before the front. This is because the speed of light is the same for
both men and during the time it takes the light to reach the ends of the carriage,
the train has travelled a certain distance forward. The light therefore strikes
the back of the carriage before the front
N.B. Even though the relative nature of space and time (encapsulated by the
Lorentz transformations) is derived from the 2nd axiom (the constant speed of
light demanded by Maxwell's equation), the cause and effect is actually the
other way around. That is, it is actually the (Lorentz) relativistic nature
of space and time, that causes an upper limit to communications (namely the
speed of light).
FIGURE 5
"All religions, arts and sciences are branches of the same tree. All these aspirations are directed toward enobling man's life, lifting it from the sphere of mere physical existence and leading the individual towards freedom" [EINSTEIN]
FIGURE 6
FIGURE 7
Moving bodies shrink and moving clocks run slower (the length must reduce in proportion to time otherwise objects would not be able to agree upon their own relative velocity). As an objects speed increases, so does its Kinetic Energy which, according to Einstein's famous equation E=mc², means that its mass also increases. [Historically it was the relativistic increase in mass, which allowed Einstein to derive his equation for mass-energy equivalence as a corollary of this relativity theory. Mass, length and time are intimately related in physical laws, hence all 3 will be affected by relativity theory and not just time and length alone.]
FIGURE 8
The
object mentioned above which is acted upon by a force F, appears to us, to be
'accelerating in slow motion' as compared to the rest frame and the force has
to be applied for longer, in order for the object to reach the velocity v, according
to our observations. We therefore conclude that is inertial mass has increased
by the same factor gamma that its clocks have slowed down. [In this thought
experiment we must stipulate that the object is being accelerated in a direction
at right angles to the motion of the moving frame]. Hence moving bodies also
increase in mass, as accommodated for in particle accelerators, (this is necessary
if the conservation of relativistic momentum is to be conserved).
Hence in summary;
1. Moving clocks run slower.
2. Moving objects contract in length.
3. Moving objects increase in mass
FIGURE 9
FIGURE 10
FIGURE 11
FIGURE 12
The following is my response to an article which claimed that Michelson-Morley' experiment did not demonstrate that the speed of light was a constant for all observers and that Einstein's theory of Relativity was flawed. It is reproduced here, as it contains useful insights into a subject that is widely known but little understood.
General Observations and Comments
Pat's article is somewhat retrograde, in that Einstein's ideas were initially
criticised very heavily by the intellectual milieu. This can be gleamed from
the fact that when he was eventually awarded the Nobel Prize, it was for his
paper on the photoelectric effect, since Relativity was still considered somewhat
contentious. Indeed one academic article listed '100 great scientists against
Einstein', his response being that if he were wrong, one such signature would
be enough. Even much later, Relativity was banned in Nazi Germany and also in
the Soviet Union during the infamous Lysenko regime. These days, manuscripts
are regularly submitted to various professors, claiming to have disproved Einstein's
most famous theory. In fact it is impossible to disprove Special Relativity,
since once one accepts the 2 fundamental axioms (namely the invariance of physical
laws for all inertial frames and secondly, the constancy of the speed of light
'c' as being one of these laws), then Relativity is logically self consistent
and therefore cannot be proved false.
Moving on to Pat's central claim that 'c' is not constant, her article suggests,
"the Earth itself cannot move quickly enough for its motion to be detectable".
In actual fact, the Michelson-Morley interferometer was perfectly sensitive
enough to detect such motion through the luminiferous Ether. Einstein was once
asked to comment upon scientific data that indicated the presence of the Ether
(the mythical medium through which light waves were originally believed to propagate).
His typically eloquent reply was "Subtle is the Lord ……. malicious
He is not". Incidentally, it is sometimes suggested that Einstein was an
atheist (c.f. Colin Wagstaff's article), but throughout his life, Einstein claimed
that his main desire was to read the mind of God. In fact one of the most well
known scientific quotes is "God does not play dice ……" hardly
the word's of an atheist, however it is no doubt true that he did not believe
in a personal God. Anyway, Einstein was a genius because he was right and as
I will briefly describe in the next section below, even when he was wrong, he
made significant contributions to our understanding of the universe.
Other scientists had tried to solve the problems/dilemmas of the day but it
took the creativity of Einstein to realise the actual truth. The Fitzgerald
contraction and the Lorentz electrodynamics of moving bodies, had offered some
explanation for the inability to detect the Ether but only Einstein realised
that the Ether did not exist and that it was our notion of space and time, which
were wrong. The equations were much the same but the physics was new, since
space and time were now relative to the speed of an observer, and they were
also inherently connected as a 4 dimensional continuum. [Indeed not only had
Lorentz already produced much of the mathematics, but Poincare had already derived
the famous equation E=MC^2 before Einstein but did not appreciate its physical
meaning in an era when nuclear energy was unknown.]
During the early years of Relativity, scientists (notably those who could not
fully comprehend Einstein's theory), tried to demonstrate ambivalences in the
theory, such as the 'Twin Paradox' or the 'Ladder in the Barn Paradox'. However
these are actually not paradoxes but serve as good illustrations of how Relativity
has to be correctly implemented. High energy particle accelerators have to be
designed so as to take such effects into account; in particular since all energy
has mass, then as the speed (and hence kinetic energy), of a particle increases,
so does its mass and hence another relativistic effect is confirmed. These effects
however, are not just confined to the esoteric domain of sub-atomic physics,
since GPS systems also have to take into account corrections due to the time
dilation cause by the high (and varying) speed of the satellite. On top of this
correction there is also the opposite effect of a faster passage of time, which
is produced in the slightly weaker gravitational field. It is interesting to
note that the first such system had an "off " switch mechanism installed,
since the technical scientists were not entirely convinced that these relativistic
effects would actually occur (such is the continuing suspicion even today).
However they needn't have bothered, as the predictions are spot-on, being accurate
to the full 13 decimal places of the atomic clock, allowing global positioning
to the nearest metre!
Finally I would also point out that when it comes to Relativity, physicists
go to great lengths to distinguish between observing as opposed to seeing. The
latter being the scientists actual basic visual data, which incorporates Doppler
shift, aberration and many other peculiar effects and illusions, that may be
seen when a spaceship goes on a high speed journey (this is what 'appears' to
an onlooker in Pat's article). What really counts in Relativity theory is what
is actually 'observed' when all these extraneous effects are stripped away,
to reveal the actual physical reality (e.g. by making corrections for the continually
increasing time delay of the light signals, as the space craft recedes).
The Science
Pat's emission phenomena (which seems to appeal somewhat to Zeno's paradox)
is not really germane to the argument, since we are really only interested in
measuring 'c' after it has left the source. The light signal could be from a
distant galaxy that is either moving away from us or towards us at great speed
- in both cases we find that 'c' is constant when measured by either 'source'
or 'observer'. In other words we cannot catch up with the light or move towards
it so as to increase the perceived speed with which it passes us. Also where
as Newton's laws were needed to describe particle motion, a wave theory invoking
a medium known as the Ether, was needed to understand light (although both were
thought to rely upon Galileo's notion of space and time). In Pat's article we
could add the speed of the bullet to that of the train but if the Earth were
travelling through the Ether, then the speed of the light wave would be found
to be smaller in its forward motion than in its opposite direction. [Sic] What
actually troubled Einstein was the very notion of catching up with an oscillating
light wave, which would then appear frozen; such a concept is not allowed in
Maxwell's laws of electromagnetism. [I will refer to this in more detail below.]
Once we accept the empirical fact that 'c' is the same for all constant relative
motion, we are forced to abolish the notion of simultaneity and hence accept
the relative nature of space and time. This can be briefly explained as follows.
Consider our train (or better still a high speed cosmic version of it), in which
an on-board observer positioned at its centre, sends out a light signal to the
front and back of the train at the same instant. From his perspective, he is
at rest and the signal arrives at the front and back simultaneously. However
from the viewpoint of an observer on the ground, whose position coincides with
that of the on-board observer at the instant that the dual signal is sent, the
light will arrive at the back of the train before the front. This is an unavoidable
consequence of the fact that each observer measures the light as travelling
at the same speed 'c'.
Henceforth we must now consider space-time as a 4 dimensional manifold, in which
different observers each slice through a different section as being their own
personal time and space, depending on their relative motion (these effects having
been empirically verified and consequently validate the second axiom). Indeed
if we generalise this so as to be compatible with gravity, this manifold has
to be extended to that of a Riemannian differential geometry, as is described
by the tensor calculus of General Relativity. Indeed Einstein was possibly his
own greatest critic, in that he realised the inadequacy of his Special theory
to operate consistently within a gravitational field. This resulted in his greatest
achievement viz. General Relativity, in which the notion of a gravitational
force is replaced by a curvature of space-time. [Intriguingly, space and time
now become of subsidiary importance compared to the reality of his field equation,
which itself exhibits a new feature known as diffeomorphism symmetry --- something
that is not a property of his Special theory.]
In fact what really influenced Einstein, was not the results of the Michelson-Morley'
experiment (he claimed that he was not aware of this at the time) but the failure
of Maxwell's equations to fit in with the classical physics of the era. Maxwell
had unified electromagnetism in a set of 4 elegant field equations, (the first
example of a unification of forces in physics) and as a corollary he determined
that light is a wave of electromagnetism, whose speed 'c' is a law of physics.
This is because the 'square of the speed of light' is equal to the reciprocal
of the 'conductivity of space' (more accurately this is the product of the permeability
and permittivity of a vacuum, these both being absolute constants for all inertial
observers). In fact the value of 'c' squared is, as we all know from E=MC^2,
the ratio of the energy of an entity divided by its mass and it is interesting
that this constant ratio is related to electromagnetism, as opposed to
the nuclear or gravitational fields. This originally led Einstein to conjecture,
that the ultimate source of all mass is electromagnetic energy, even when locked
up within conventional matter. [More recently when considering the strong nuclear
force, much of the actual mass of a proton or neutron is due to the quantum
chromodynamic energy of the gluon field, rather than just the mass of the constituent
quarks]
It was therefore this electromagnetic aspect that really troubled Einstein and
more specifically, he realised that Maxwell's equations do not transform in
the same way as Newton's equations, which conformed to the notion of absolute
space and universal time. A conflict was therefore brought to light (excuse
the pun) and Einstein realised that either Newton's laws were intrinsically
wrong or Maxwell's laws were at fault. Einstein, although the greatest admirer
of Newton's work, chose Maxwell's equations as being intrinsically correct -
they were in fact the first ever equations to satisfy Special Relativity and
transform according to Einstein's notion of space and time (i.e. Lorentz covariant).
With the same stroke Einstein cut away the Ether from Maxwell's field equations,
allowing them to stand as real independent entities, with their own faithful
representation of space-time symmetries
As mentioned above, I will now briefly deal with some of Einstein's actual shortcomings.
Firstly quantum theory; although originally one of the early proponents (cf.
photoelectric effect), Einstein later became its greatest critic. However his
famous debates with Niel's Bohr did result in a greater clarification of what
was a tumultuous time in physics. Secondly his 'greatest blunder', the introduction
of a cosmological constant. Ironically we have recently detected acceleration
in the expansion of the universe, which alludes to a dark energy that can be
associated to such a cosmological constant. [Incidentally this recessional
velocity can, for very distant galaxy clusters, be actually greater than 'c'
due to the expansion of space itself. However this does not transgress
the second axiom, since the speed of light through space is still 'c'].
Finally Einstein's unfinished symphony, in which he tried in vain to unify electromagnetism
with his General theory of Relativity (i.e gravity). He initially considered
Kaluza's 5 dimensional tensor theory and also Klein's compactification of the
extra dimension, as well as Weyl's gauge transformation (techniques that are
commonplace in modern string theories). His best attempt involved the application
of 'distant parallelism' or 'vierbeins', which concentrates on the connection
aspect of differential geometry, instead of the usual metric theory employed
in General Relativity. Although a failure, this technique is another tool that
is utilised in modern theories of quantum gravity and yet again shows the legacy
of even his unsuccessful efforts.
I would like to conclude with what are seriously considered to be possible inadequacies
of Relativity theory. Firstly there are theories that incorporate a change in
the value of 'c' over the early history of the universe, which relate to a large
decrease in the cosmological constant over this period. This however may not
be in direct conflict with the essence of General Relativity, which only requires
that 'c' is locally constant in space-time. Secondly there are suggestions that
'c' needs to increase when we consider extremely high energy interactions, otherwise
approaching photons would become blue shifted to beyond the acceptable Planck
mass/energy limit. This would be a more serious challenge but we would then
be moving into the realm of quantum gravity, where most physicists believe that
Relativity theory would be inapplicable in its present form. [Indeed General
Relativity contains the seeds of its own destruction, in the form of a singularity
at the centre of a black hole - Einstein himself did not believe that such stellar
objects could actually exist.] Finally, it has been conjectured in string theory
that an asymmetry*!* in space, may have been singled
out during the compactification of dimensions that occurred in the early universe.
The consequence of this would mean that although an observer's frame of reference
would have an overall Lorentz covariance, a particle's frame might exhibit a
small preference of direction. Efforts are continually being made to test these
and other ideas, to see if there are any lacunae in Einstein's theory. However,
as exemplified by a recent Nobel Prize (awarded for the detection of predicted
gravitational radiation from binary stars), General Relativity is the most accurate
theory known to man and as Einstein once controversially declared " my
equations are too beautiful to be false"
*!* The action of any physical theory can be written in a reparametrisation invariant way. This formal diffeomorphism symmetry is, in general, obtained at the expense of introducing absolute objects into the theory. [An absolute object is one which is defined to be a function with one or more components, of space-time that is not dependent on the state of matter, such as 'a prior' geometry that is fixed immutably]. The special diffeomorphisms, corresponding to the Poincare transformations, only generates a true Poincare symmetry if the absolute objects are invariant under these transformations. The basic idea, for deriving Poincare (and hence Lorentz) invariance from diffeomorphism symmetry, is then to find dynamical, quantum mechanical arguments for potential absolute objects being Poincare invariant or non-existent. It has also been suggested by some, that symmetry is not a fundamental property of the laws of physics but that it appears only at an infra-red level i.e. low energy. If we consider the most general renormalisable Poincare action for a spinless field then by dimensional counting, renormalisibility requires that there is no coefficient in the Lagrangian having dimension of mass to a negative power. [This requirement prevents the occurrence of terms with gradients other than the usual kinetic energy term]. It then follows that the action must be invariant under the parity operation. The existence of a renormalisable field theory for the spinless fields therefore plays a crucial role in the above derivation of parity symmetry. If however the spinless particles were not really fundamerntal but only bound states, then our Lagrangian would become an effective Lagrangian not constrained by renormalisibility. The allowed existence of certain effective terms, would mean that the parity operation was only an approximate symmetry at low energies but not one which is intrinsic to the theory or observable at high eneries! In other words more complicated Lagrangian terms involving bound states, may allow more flexibility than the renormalisibility constraint but the symmetries are not obeyed except at low energy.
* * * * * * * * * * * * * * * * *
Some Speculations on time travel and GR
There have been several speculations as to the possibility of time travel most of which rely on the notion of warped space time. Special relativity is itself completely consistent with time travel into the future (moving clocks run slower**) but traveling into the past could lead to paradoxes. If a man can travel into the past he could change events (e.g. kill his grandfather) which would prevent him from ever being born in the first place. In 1949 Kurt Godel found a solution to Einstein's field equations, in which a static universe would be stable providing it rotated sufficiently fast (the centripetal acceleration is in balance with the gravitational attraction of the whole mass in the universe). He found that such a universe would result in a curving around of space-time in such a way that traveling in closed loops, would not only change your displacement but would also allow you to travel backwards in time. Since a rotating inverse is not the case, the next best option is inside a spherical black hole (which are believed to be quite common), where the space and time coordinates also become interchanged. However there is no way of escaping from a spherical black whole once you have passed the event horizon.
There may however be a way to circumvent this problem, if one could create a rotating cylindrical shaped black hole, whose rotation would allow you to escape from being dragged down into the singularity, but such structures may not be stable. Also there are worm holes that allow distant regions of space to be locally connected by a short cut through space and which also suggest the feasibility of backwards time travel, however these structures are also believed to be fundamentally unstable for any would be time traveler. Another possibility arises from the study of cosmic strings; when two such entities come together it can be shown from topological considerations that it may be possible to travel backwards in time by moving in a circular path around the 2 strings. However such cosmic strings have not yet been identified in the universe. Also any such time travel machine would only allow you to travel back to the time in which the devise was first built - this is often cited as the reason why we have not been visited by a more advanced civilization from our future. As already mention backward time travel can lead to dilemmas. For example imagine that one day a girl physicist discovers a new solution written by Einstein, which describes the workings of a feasible time machine. Having the technology to produce such a machine, she travels back in time to visit Einstein and shows him the solution which he then records (and is subsequently discovered by the girl). The paradox then arises as to who actually discovered the solution! Finally an interesting scenario has been put forward concerning the rapid expansion in computer technology. Future civilizations will have sufficient computer power (especially with the advent of quantum computers) to create perfect virtual reality universes, which they will be able to run backwards and forwards in time. Indeed they would quite easily be able to run millions of such universe in parallel, each of which permits time travel for those in control. We then arrive at the disturbing realization that, statistically speaking, ours is more likely to be one of these virtual universe set in the past, rather than being the actual real universe which exists only for this one future civilization (also we are clearly not sufficiently advanced to be that universe).
** This time dilation effect has been accurately verified on many occasion. Specifically for man it has been estimated that the worlds most experienced cosmonaut has reduced his aging by one fiftieth of a second as a result of all his time spent orbiting the Earth. This has been calculated based on the speed at which he has been traveling (producing a minute reduction in the passage of time) and also the reduced gravitational field compare to that at the actual surface of the Earth (this causes an even smaller speeding up of the flow of time).
*********************************
A Synopsis of Hawking view on the Information Paradox
Preamble
Hawkings originally showed that the area of a black hole can never decrease
in time, suggesting that it is analogous to entropy. Bekenstein argued that
this relationship was more than just an an analogy and that a black hole has
an actual entropy that is proportional to its area. However entropy is related
to temperature (~S = ~Q/T)and this was not a property that was associated to
black holes at that time. Hawkings then went on to discover that a black hole
emits radiation and can be given a temperature that is inversely proportional
to its mass (and the mass of a black hole directly determines its event horizon).
Hence the entropy of a black hole can be shown to be S =1A/4hG and when object
fall into a black hole the entropy of the surrounding universe decreases (since
negentropy is a measure of information which is reduced when objects disappear,)
while that of the black hole increases so as to maintain/increase the overall
value. On the other hand if the black hole radiates energy, it loses surface
area and hence entropy but the entropy of the outside world will increase to
make up for it. However the entropy that is removed when a highly organized
system is dropped into a black hole, is much less that the increase of entropy
that is returned, when the black hole radiates that amount of mass back to the
universe, thus implying an overall increase in entropy, in keeping with the
second law of thermodynamics. Bekenstein later went on to assert that the amount
of information that can be contained in a region is not only finite but is proportional
to the area bounded by that region, measured in Planck units (Holographic
principle) and this implies that the universe must be discrete on the Planck
scale. This Bekenstein Bound is partly a consequence of GR and the 2nd
law of Thermodynamics, but the argument can be turned around, and it can be
shown that assuming the 2nd law and the Bekenstein Bound, it is possible to
derive GR. Hence we have 3 approaches to combining GR with QT viz String theory,
LQG, and black hole thermodynamics and each of these indicate (in differing
ways) that space and time are discrete (the last two are also relational based).
More recently, new difficulties have become evident, from the fact that when
(organized) objects drop into a black hole, their quantum wave functions are
in a pure (correlated) state, while when the Black Hole eventually evaporates,
the radiation is in a mixed quantum state (i.e. the individual quanta are not
correlated as in an assembly of bosons or fermions). Now a pure state
cannot evolve into a mixed state by means of a unitary transformation,
which is a problem since unitary transformations are a crucial feature of all
quantum wavefunctions (in order that probabilities evolve in a correct manner).
Hence we need to find a way of reconciling this dilemma, perhaps by invoking
a non unitary theory or by discovering a way of accounting for the extra information
that a pure state has in comparison to a mixed state. If the correlations between
the inside and outside of the black hole are not restored during the evaporation
process, then by the time that the black hole has evaporated completely, an
initial pure state will have evolved to a mixed state, i.e., "information"
will have been lost. For this reason, the issue of whether a pure state can
evolve to a mixed state in the process of black hole formation and evaporation
is usually referred to as the "black hole information paradox". [There
are in fact two logically independent grounds for the claim that the evolution
of an initial pure state to a final mixed state is in conflict with quantum
mechanics:
1. Such evolution is asserted to be incompatible with the fundamental principles
of quantum theory, which postulates a unitary time evolution of a state vector
in a Hilbert space.
2. Such evolution necessarily gives rise to violations of causality and/or energy-momentum
conservation and, if it occurred in the black hole formation and evaporation
process, there would be large violations of causality and/or energy-momentum
(via processes involving virtual black holes) in ordinary laboratory physics.
Some advocate that a black hole cannot completely disappear but that some of the original information persists as a kind of nugget. Others believe that this information is re-emitted as some form of correlated particles. Another view is that a new quantum theory of gravity will necessarily be non unitary. Hawking has changed his original view that information is lost and now advocate that the actual probability of sub atomic(and virtual) black holes actually causing the loss of information is minuscule and that unitarity is only violated in a mild sense. [He proposes that in the presence of black holes, the quantum state of a system evolves into a (non-pure state) density matrix --- a la von Neumann] This is somewhat analogous to the improbable effect in the violation of the 2nd law of thermodynamics or the approach to decoherence in QT. In effect the sum over all the possible histories (geometries) of the universe, results in the nullification of the non unitary effect of black holes in the long term. Susskind on the other hand has applied t' Hooft's holographic principle to sting theory and believes that the information is stored in the horizon of a black hole [Indeed using string theory to calculate the possible configurations of black holes has reproduced the BH formula for its entropy -- as have LQG calculations]. This has been strengthened more recently by Maldacinas conjecture (AdS/CFT correspondence), which demonstrates that there is an equivalence between the string theory of gravity in a 5D anti-de Sitter universe and the conformal supersymmetric Yang- Mills theory on its horizon [This holographic duality becomes more precise the larger the value of supersymmetry N]. Maldacina's conjecture not only says that gravity is in some deep way the same as quantum field theory but also implements the holographic principle in a concrete way.
The following is an extract of Hawking's presentation in Dublin in 2004 (the additional commentry in blue is by John. Baez) Confer with.the quantum section for more detail
"The black hole information paradox started in 1967, when Werner Israel
showed that the Schwarzschild metric,
was the only static vacuum black hole solution. This was then generalized to
the no hair theorem: the only
stationary rotating black hole solutions of the Einstein-Maxwell equations are
the Kerr-Newman metrics. The no
hair theorem implied that all information about the collapsing body was lost
from the outside region apart from
three conserved quantities: the mass, the angular momentum, and the electric
charge.
This loss of information wasn't a problem in the classical theory. A classical
black hole would last for ever, and the
information could be thought of as preserved inside it, but just not very accessible.
However, the situation
changed when I discovered that quantum effects would cause a black hole to radiate
at a steady rate. At least in
the approximation I was using, the radiation from the black hole would be completely
thermal, and would carry no
information. So what would happen to all that information locked inside a black
hole, that evaporated away, and
disappeared completely? It seemed the only way the information could come out
would be if the radiation was not
exactly thermal, but had subtle correlations. No one has found a mechanism to
produce correlations, but most
physicists believe one must exist. If information were lost in black holes,
pure quantum states would decay into
mixed states, and quantum gravity wouldn't be unitary."
Hawking is studying the process of creating a black hole
and letting it evaporate away. He's imagining studying this in the usual style
of particle physics, as a "scattering experiment", where we throw
in a bunch of particles and see what comes out. Here we throw in a bunch of
particles, let them form a black hole, let the black hole evaporate away, and
examine the particles (typically
photons for the most part) that shoot out. The rules of the game in a "scattering
experiment" are that we can only talk about what's going on "at infinity",
meaning very far from where the black hole forms - or more precisely, where
it may or may not form! The advantage of this is that physics at infinity can
be described without the full machinery of quantum gravity: we don't have to
worry about quantum fluctuations of the geometry of spacetime messing up our
ability to say where things are. The
disadvantage is that we can't actually say for sure whether or not a black hole
formed. At least this seems like a "disadvantage"
at first - but a better term for it might be a "subtlety", since it's
crucial for resolving the puzzle: [JB]
"I first raised the question of information loss in '75, and the argument
continued for years, without any resolution
either way. Finally, it was claimed that the issue was settled in favour of
conservation of information, by
AdS/CFT. AdS/CFT is a conjectured duality between supergravity in anti-deSitter
space and a conformal field
theory on the boundary of anti-deSitter space at infinity. Since the conformal
field theory is manifestly unitary, the
argument is that supergravity must be information preserving. Any information
that falls in a black hole in
anti-deSitter space, must come out again. But it still wasn't clear how information
could get out of a black hole. It
is this question I will address.
Black hole formation and evaporation can be thought of as a scattering process.
One sends in particles and
radiation from infinity, and measures what comes back out to infinity. All measurements
are made at infinity, where
fields are weak, and one never probes the strong field region in the middle.
So one can't be sure a black hole
forms, no matter how certain it might be in classical theory. I shall show that
this possibility allows information to
be preserved and to be returned to infinity."
Now, the way Hawking likes to calculate things in this
sort of problem is using a "Euclidean path integral". This is a rather
controversial approach - hence his grin when he said it's the "only sane
way" to do these calculations - but let's not worry about
that. Suffice it to say that we replace the time variable "t" in all
our calculations by "it", do a bunch of calculations, and then
replace "it" by "t" again at the end. This trick is called
"Wick rotation". In the middle of this process, we hope all our formulas
involving the geometry of 4d spacetime have magically become formulas involving
the geometry of 4d space. The answers to
physical questions are then expressed as integrals over all geometries of 4d
space that satisfy some conditions depending on the
problem we're studying. This integral over geometries also includes a sum over
topologies.[JB]
"I adopt the Euclidean approach, the only sane way to do quantum gravity
non-perturbatively. [He grinned at this
point.] In this, the time evolution of an initial state is given by a path integral
over all positive definite metrics that
go between two surfaces that are a distance T apart at infinity. One then Wick
rotates the time interval, T, to the
Lorentzian.
The path integral is taken over metrics of all possible topologies that fit
in between the surfaces. There is the trivial
topology: the initial surface cross the time interval. Then there are the nontrivial
topologies: all the other possible
topologies. The trivial topology can be foliated by a family of surfaces of
constant time. The path integral over all
metrics with trivial topology, can be treated canonically by time slicing. In
other words, the time evolution
(including gravity) will be generated by a Hamiltonian. This will give a unitary
mapping from the initial surface to
the final."
Unfortunately, nobody knows how to define these integrals.
However, physicists like Hawking are usually content to compute
them in a "semiclassical approximation". This means integrating not
over all geometries, but only those that are close to some
solution of the classical equations of general relativity. We can then do a
clever approximation to get a closed-form answer. (Note: here I'm talking about
the equations of general relativity on 4d space, not 4d spacetime. That's because
we're in
the middle of this Wick rotation trick.) Actually, I'm oversimplifying a bit.
We don't get "the answer" to our physics question this way: we get
one answer for each solution of the equations of general relativity that we
deem relevant to the problem at hand. To finish the job, we should add up all
these partial answers to get the total answer. But in practice this last step
is always too hard: there are too many topologies, and too many classical solutions,
to keep track of them all. So what do we do? We just add up a few of the answers,
cross our fingers, and hope for the best! If this procedure offends you, go
do something easy like math. In the problem at hand here, Hawking focuses on
two classical solutions, or more precisely two classes of them. One describes
a spacetime with no black hole, the other describes a spacetime with a black
hole which lasts forever. Each one gives a contribution to the semiclassical
approximation of the integral over all geometries. To get answers to physical
questions, he needs to sum over both. In principle he should sum over infinitely
many others, too, but nobody knows how, so he's probably hoping the crux of
the problem can be understood by considering just these two.
He says that if you just do the integral over geometries
near the classical solution where there's no black hole, you'll find -
unsurprisingly - that no information is lost as time passes. He also says that
if you do the integral over geometries near the classical solution where there
is a black hole, you'll find -surprisingly - that the answer is zero for a lot
of questions you can measure the answers to far from the black hole. In physics
jargon, this is because a bunch of "correlation functions decay exponentially".
So, when you add up both answers to see if information is lost in the real problem,
where you can't be sure if there's a black hole or not, you get the same answer
as if there were no black hole! [JB]
"The nontrivial topologies cannot be foliated by a family of surfaces
of constant time. There will be a fixed point in
any time evolution vector field on a nontrivial topology. A fixed point in the
Euclidean regime corresponds to a
horizon in the Lorentzian. A small change in the state on the initial surface
would propagate as a linear wave on the
background of each metric in the path integral. If the background contained
a horizon, the wave would fall through
it, and would decay exponentially at late time outside the horizon. For example,
correlation functions decay
exponentially in black hole metrics. This means the path integral over all topologically
nontrivial metrics will be
independent of the state on the initial surface. It will not add to the amplitude
to go from initial state to final that
comes from the path integral over all topologically trivial metrics. So the
mapping from initial to final states, given
by the path integral over all metrics, will be unitary.
One might question the use in this argument, of the concept of a quantum state
for the gravitational field on an
initial or final spacelike surface. This would be a functional of the geometries
of spacelike surfaces, which is not
something that can be measured in weak fields near infinity. One can measure
the weak gravitational fields on a
timelike tube around the system, but the caps at top and bottom, go through
the interior of the system, where the
fields may be strong.
One way of getting rid of the difficulties of caps would be to join the final
surface back to the initial surface, and
integrate over all spatial geometries of the join. If this was an identification
under a Lorentzian time interval, T, at
infinity, it would introduce closed timelike curves. But if the interval at
infinity is the Euclidean distance, beta, the
path integral gives the partition function for gravity at temperature 1/beta.
The partition function of a system is the trace over all states, weighted
with e-beta H. One can then integrate beta
along a contour parallel to the imaginary axis with the factor e-beta E. This
projects out the states with energy E0.
In a gravitational collapse and evaporation, one is interested in states of
definite energy, rather than states of
definite temperature.
There is an infrared problem with this idea for asymptotically flat space.
The Euclidean path integral with period
beta is the partition function for space at temperature 1/beta. The partition
function is infinite because the volume
of space is infinite. This infrared problem can be solved by a small negative
cosmological constant. It will not
affect the evaporation of a small black hole, but it will change infinity to
anti-deSitter space, and make the thermal
partition function finite.
The boundary at infinity is then a torus, S1 cross S2. The trivial topology,
periodically identified anti-deSitter
space, fills in the torus, but so also do nontrivial topologies, the best known
of which is Schwarzschild
anti-deSitter. Providing that the temperature is small compared to the Hawking-Page
temperature, the path
integral over all topologically trivial metrics represents self-gravitating
radiation in asymptotically anti-deSitter
space. The path integral over all metrics of Schwarzschild AdS topology represents
a black hole and thermal
radiation in asymptotically anti-deSitter.
The boundary at infinity has topology S1 cross S2. The simplest topology that
fits inside that boundary is the trivial
topology, S1 cross D3, the three-disk. The next simplest topology, and the first
nontrivial topology, is S2 cross D2.
This is the topology of the Schwarzschild anti-deSitter metric. There are other
possible topologies that fit inside
the boundary, but these two are the important cases: topologically trivial metrics
and the black hole. The black
hole is eternal. It cannot become topologically trivial at late times.
In view of this, one can understand why information is preserved in topologically
trivial metrics, but exponentially
decays in topologically non trivial metrics. A final state of empty space without
a black hole would be
topologically trivial, and be foliated by surfaces of constant time. These would
form a 3-cycle modulo the
boundary at infinity. Any global symmetry would lead to conserved global charges
on that 3-cycle. These would
prevent correlation functions from decaying exponentially in topologically trivial
metrics. Indeed, one can regard
the unitary Hamiltonian evolution of a topologically trivial metric as the conservation
of information through a
3-cycle.
On the other hand, a nontrivial topology, like a black hole, will not have
a final 3-cycle. It will not therefore have
any conserved quantity that will prevent correlation functions from exponentially
decaying. One is thus led to the
remarkable result that late time amplitudes of the path integral over a topologically
non trivial metric, are
independent of the initial state. This was noticed by Maldacena in the case
of asymptotically anti-deSitter in 3d,
and interpreted as implying that information is lost in the BTZ black hole metric.
Maldacena was able to show that
topologically trivial metrics have correlation functions that do not decay,
and have amplitudes of the right order to
be compatible with a unitary evolution. Maldacena did not realize, however that
it follows from a canonical
treatment that the evolution of a topologically trivial metric, will be unitary.
So in the end, everyone was right, in a way. Information is lost in topologically
nontrivial metrics, like the eternal
black hole. On the other hand, information is preserved in topologically trivial
metrics. The confusion and paradox
arose because people thought classically, in terms of a single topology for
spacetime. It was either R4, or a black
hole. But the Feynman sum over histories allows it to be both at once. One can
not tell which topology
contributed the observation, any more than one can tell which slit the electron
went through, in the two slits
experiment. All that observation at infinity can determine is that there is
a unitary mapping from initial states to
final, and that information is not lost.
My work with Hartle showed the radiation could be thought of as tunnelling
out from inside the black hole. It was
therefore not unreasonable to suppose that it could carry information out of
the black hole. This explains how a
black hole can form, and then give out the information about what is inside
it, while remaining topologically trivial.
There is no baby universe branching off, as I once thought. The information
remains firmly in our universe. I'm
sorry to disappoint science fiction fans, but if information is preserved, there
is no possibility of using black holes
to travel to other universes. If you jump into a black hole, your mass-energy
will be returned to our universe, but
in a mangled form, which contains the information about what you were like,
but in an unrecognisable state.
There is a problem describing what happens, because strictly speaking the
only observables in quantum gravity
are the values of the field at infinity. One cannot define the field at some
point in the middle, because there is
quantum uncertainty in where the measurement is done. However, in cases in which
there are a large number, N,
of light matter fields, coupled to gravity, one can neglect the gravitational
fluctuations, because they are only one
among N quantum loops. One can then do the path integral over all matter fields,
in a given metric, to obtain the
effective action, which will be a functional of the metric.
One can add the classical Einstein-Hilbert action of the metric to this quantum
effective action of the matter fields.
If one integrated this combined action over all metrics, one would obtain the
full quantum theory. However, the
semiclassical approximation is to represent the integral over metrics by its
saddle point. This will obey the Einstein
equations, where the source is the expectation value of the energy momentum
tensor, of the matter fields in their
vacuum state.
The only way to calculate the effective action of the matter fields, used
to be perturbation theory. This is not likely
to work in the case of gravitational collapse. However, fortunately we now have
a non-perturbative method in
AdS/CFT. The Maldacena conjecture says that the effective action of a CFT on
a background metric is equal to
the supergravity effective action of anti-deSitter space with that background
metric at infinity. In the large N limit,
the supergravity effective action is just the classical action. Thus the calculation
of the quantum effective action of
the matter fields, is equivalent to solving the classical Einstein equations.
The action of an anti-deSitter-like space with a boundary at infinity would
be infinite, so one has to regularize.
One introduces subtractions that depend only on the metric of the boundary.
The first counter-term is proportional
to the volume of the boundary. The second counter-term is proportional to the
Einstein-Hilbert action of the
boundary. There is a third counter-term, but it is not covariantly defined.
One now adds the Einstein-Hilbert
action of the boundary and looks for a saddle point of the total action. This
will involve solving the coupled four-
and five-dimensional Einstein equations. It will probably have to be done numerically.
In this talk, I have argued that quantum gravity is unitary, and information
is preserved in black hole formation and
evaporation. I assume the evolution is given by a Euclidean path integral over
metrics of all topologies. The
integral over topologically trivial metrics can be done by dividing the time
interval into thin slices and using a linear
interpolation to the metric in each slice. The integral over each slice will
be unitary, and so the whole path integral
will be unitary.
On the other hand, the path integral over topologically nontrivial metrics,
will lose information, and will be
asymptotically independent of its initial conditions. Thus the total path integral
will be unitary, and quantum
mechanics is safe.
It is great to solve a problem that has been troubling me for nearly thirty
years, even though the answer is less
exciting than the alternative I suggested. This result is not all negative however,
because it indicates that a black
hole evaporates, while remaining topologically trivial. However, the large N
solution is likely to be a black hole
that shrinks to zero. This is what I suggested in 1975. " [S. Hawking]
As he points out, the answers to a bunch of questions
diverge unless we put our black hole in a box of finite size. A convenient
way to do this is to introduce a small negative cosmological constant, which
changes our default picture of spacetime from
Minkowski spacetime, which is topologically R4, to anti-deSitter spacetime,
which is topologically R x D3 after we add the
"boundary at infinity". Here R is time and the 3-disk D3 is space.
This is a Lorentzian manifold with boundary, but when we do
Wick rotation we get a Riemannian manifold with boundary having the same topology.
However, when we are doing Euclidean path integrals at
nonzero temperature, we should replace the time line R here by a
circle whose radius is the reciprocal of that temperature. (Take my word for
it!) So now our Riemannian manifold with
boundary is S1 x D3. This is what Hawking uses to handle the geometries without
a black hole. The boundary of this manifold is S1 x S2. But there's another
obvious manifold with this boundary, namely D2 x S2 And this corresponds to
the geometries with a black hole!
In his talk, Hawking points out that S1 x D3 has a nontrivial
3-cycle in it if we use relative cohomology and work relative to the
boundary S1 x S2. But, D2 x S2 does not. When spacetime is n-dimensional, conservation
laws usually come from integrating
closed (n-1)-forms over cycles that correspond to "space", so we get
interesting conservation laws when there are nontrivial
(n-1)-cycles. Here Hawking is using this to argue for conservation of information
when there's no black hole - namely for S1 x
D3 - but not when there is, namely for D2 x S2.
All this is fine and dandy; the hard part is to see why
the case when there is a black hole doesn't screw things up! This is where
his allusions to "exponentially decaying correlation functions come in"
- and this is where I'd like to see more details. I guess a
good place to start is Maldacena's papers on the black hole in 3d spacetime
- the so-called Banados-Teitelboim-Zanelli or
"BTZ" black hole. This is a baby version of the problem, one dimension
down from the real thing, where everything should get
much simpler. [JB]
Below is a (Ghost View) file extract from "The Nature of Space & Time" (S. Hawking & R. Penrose)